Cite this Article
Khaled HAZAYMEH, Quazi K HASSAN. , A remote sensing-based agricultural drought indicator and its implementation over a semi-arid region, Jordan. Journal of Arid Land, 2017, 9(3): 319-330.  
Permissions
Copyright©2017, Journal of Arid Land
Received:2016-07-02 Revised:2017-04-07
A remote sensing-based agricultural drought indicator and its implementation over a semi-arid region, Jordan
Khaled HAZAYMEH1,2, Quazi K HASSAN1,*
1 Department of Geomatics Engineering, Schulich School of Engineering, University of Calgary, Calgary, Alberta, Canada
2Department of Geography, Faculty of Arts, Yarmouk University, Irbid 21163, Jordan
*Corresponding author: Quazi K HASSAN (E-mail: qhassan@ucalgary.ca)
Abstract

The objective of the study was to develop a remote sensing (i.e., Landsat-8 and MODIS)-based agricultural drought indicator (ADI) at 30-m spatial resolution and 8-day temporal resolution and also to evaluate its performance over a heterogeneous agriculture dominant semi-arid region in Jordan. Firstly, we used principal component analysis (PCA) to evaluate the correlations among six commonly used remote sensing-derived agricultural drought related variables. The variables included normalized difference water index (NDWI), normalized difference vegetation index (NDVI), visible and shortwave drought index (VSDI), normalized multiband drought index (NMDI), moisture stress index (MSI), and land surface temperature (LST). Secondly, we integrated the relatively less correlated variables (that were found to be NDWI, VSDI, and LST) to generate four agricultural drought categories/conditions (i.e., wet, mild drought, moderate drought, and severe drought). Finally, we evaluated the ADI maps against a set of 8-day ground-based standardized precipitation index values (i.e., SPI-1, SPI-2, …, SPI-8) by use of confusion matrices and observed the best results for SPI-4 (i.e., overall accuracy and Kappa-values were 83% and 76%, respectively) and SPI-5 (i.e., overall accuracy and Kappa-values were 85% and 78%, respectively). The results demonstrated that the method would be valuable for monitoring agricultural drought conditions in semi-arid regions at both a reasonably high spatial resolution (i.e., 30-m) and a short time period (i.e., 8-day).

Key words: spatio-temporal image fusion model (STI-FM); land surface temperature (LST); surface reflectance; standardized precipitation index (SPI); Landsat-8; MODIS
1 Introduction

Agricultural drought is a natural hazard that usually occurs when the available water content goes below the optimal needs of the proper growth of plants during its growing season (Wilhite et al., 2007). In monitoring agricultural drought, one of the most commonly employed methods is the use of ground-based hydro-meteorological variables (e.g., precipitation, temperature, evaporation, and soil moisture). Some examples of the variables include: (i) Palmer drought severity index (PSDI) that uses precipitation and temperature (Palmer, 1965); (ii) crop moisture index (CMI) that incorporates soil moisture, precipitation, and temperature (Palmer, 1968); (iii) crop water stress index (CWSI) that is based on actual and potential evaporation (Jackson et al., 1981); (iv) standardized precipitation index (SPI) that uses precipitation regimes (Mckee et al., 1993); and (v) multivariate standardized drought index (MSDI) that employs soil moisture and precipitation (Hao and AghaKouchak, 2013). These indices usually provide very accurate estimates of agricultural drought conditions at the point locations. However, the uneven spatial distribution of the hydro-meteorological stations across the landscape often results uncertainties in delineating spatial context. In order to address these uncertainties, geographic information system (GIS)-based interpolation techniques (e.g., inverse distance, Krigging, nearest neighbor, etc.) are usually employed. These techniques often generate less-certain outcomes because the input variables for the interpolation are often obtained from limited point locations (Li and Heap, 2014).

In order to address the above-mentioned issues, one of the alternates is the use of remote sensing techniques (Hao et al., 2014; AghaKouchak et al., 2015; Hazaymeh and Hassan, 2016). In general, such approaches are developed on the basis of exploiting one or more of the following criteria. Firstly, vegetation greenness-related variables (e.g., normalized difference vegetation index (NDVI), enhanced vegetation index (EVI), modified perpendicular drought index (MPDI), vegetation condition index (VCI), etc.) were derived as a function of visible and near infrared (NIR) spectral bands. Such approaches were widely used in monitoring drought conditions over various ecosystems across the world (Tucker and Choudhury, 1987; Kogan, 2002; Samanta et al., 2011; Shahabfar et al., 2012; Zhou and Lyu, 2016). Secondly, meteorology-related variables (e.g., temperature condition index (TCI), normalized difference temperature index (NDTI), etc.) were calculated using thermal spectral band-derived land surface temperature (LST) and used in assessing vegetation water stress and drought monitoring (McVicar and Jupp, 1998; Kogan, 2002). Thirdly, surface wetness conditions were derived in two ways. The first one was based on exploiting inherent relationship between surface temperature and vegetation greenness and some examples include temperature-vegetation dryness index (TVDI), vegetation temperature condition index (VTCI), evaporative stress index (ESI), temperature-vegetation index (TVX), etc. (Lambin and Ehrlich, 1996; Sandholt et al., 2002; Anderson et al., 2011). The second one was based on integrated visible, NIR, and shortwave infrared (SWIR) spectral bands. And some examples include reduced simple ratio (RSR), visible and shortwave infrared drought index (VSDI), four bands drought index (FBDI), moisture adjusted vegetation index (MAVI), etc. (Brown et al., 2000; Zhang et al., 2013; Zhu et al., 2014; Ranjan, 2015). Fourthly, vegetation wetness indices (e.g., moisture stress index (MSI), normalized difference water index (NDWI), normalized multiband drought index (NMDI), etc.) were derived from NIR and SWIR spectral bands; and were used to comprehend drought conditions through the vegetation moist status (Hunt and Rock, 1989; Gao, 1996; Chowdhury and Hassan, 2015).

In general, there are several issues in case of implementing a single one of the above-mentioned criteria in agricultural drought monitoring. Firstly, vegetation greenness-related variables showed an apparent time lag in responding to water stress (Gao, 1996; Chakraborty and Sehgal, 2010). In addition, they were unable to accurately reflect the actual water condition in vegetation as different factors might affect the vegetation status, such as phenology, insects, vegetation type, temperature, and chlorophyll (Anjum et al., 2011). Secondly, meteorological variables were affected by sensor configurations, derivation algorithm, and heterogeneity of landscape (Benmecheta et al., 2013). Thirdly, the computation of wetness surface condition-related variables was complicated and highly dependent on the researcher personal skills and image specific date (Wang et al., 2011) and topography (Akther and Hassan, 2011a). Fourthly, vegetation wetness indices were affected by land cover types, vegetation intensity, and land surface heterogeneity (Ghulam et al., 2008). Therefore, a combination of remote sensing-based variables from different approaches might provide more comprehensive assessment of drought conditions (Jang et al., 2006; Gu et al., 2008). For example, Kogan (2002) combined VCI (i.e., vegetation greenness) and TCI (i.e., meteorological variable) to calculate vegetation health index (VHI). Another example came from Jang et al. (2006) and Gu et al. (2008) who calculated normalized moisture index (NMI) and normalized difference drought index (NDDI), respectively, as a function of combining NDWI (i.e., vegetation wetness) and NDVI (i.e., vegetation greenness). It would be worthwhile to mention that the combination approach was also applied in other water stress related applications. For example, the combination approach was employed to forecast forest fire danger conditions (Akther and Hassan, 2011b; Chowdhury and Hassan, 2013, 2015). In those cases, three combinations were adopted: (i) LST, NMDI, and temperature-vegetation wetness index (TVWI) (Akther and Hassan, 2011b); (ii) LST, NMDI, and NDVI (Chowdhury and Hassan, 2013); and (iii) LST, NMDI, NDVI, and perceptible water (PW) (Chowdhury and Hassan, 2015). However, in the previous studies, the relationships among the input variables were neglected despite the possibilities of having high correlations among input variables. In fact, such correlations might potentially generate uncertainties in model outputs (Jensen, 2005). In addition, synergy between remote sensing and other data types was also reported in the literature, such as vegetation drought response index (VegDRI; Brown et al., 2013), integrated surface drought index (ISDI; Wu et al., 2013), and US drought monitor (USDM; Svoboda et al., 2002).

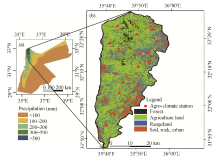
In this study, our objective was to develop a fully remote sensing-based method for monitoring agricultural drought conditions and to evaluate its performance over a semi-arid heterogeneous rainfed agricultural dominant landscape in Jordan, Middle East. In general, remote sensing data having both high spatial and temporal resolutions would be required for evaluating agricultural drought conditions, as agriculture land cover would be relatively heterogeneous and having small areas and as drought could often occur during critical short time spans during the growing season (Wu and Wilhite, 2004). Thus, we opted to implement a spatio-temporal image-fusion model (STI-FM) described in Hazaymeh and Hassan (2015a, b) to generate synthetic Landsat-8 like data with 30-m spatial and 8-day temporal resolutions upon combing regular Landsat-8 (having 30-m spatial resolution with 16-day temporal resolution) with Moderate-Resolution Imaging Spectroradiometer (MODIS)-based 8 day composite data having 250-1000 m spatial resolutions. Then, we used these fused data for developing our method. The development of the method consisted of three specific steps. Firstly, we evaluated the correlations among a set of remote sensing-based variables (including NDWI, NMDI, NDVI, MSI, VSDI, and LST) usually employed in assessing agricultural drought conditions to determine relatively less correlated ones. In this context, we employed the most commonly-used methods, such as principal component analysis (PCA; Jensen, 2005; Akbar et al., 2011). Secondly, we employed these relatively less correlated set of variables for developing a remote sensing-based agricultural drought indicator (ADI) upon adopting the forest fire danger forecasting framework described in Akther and Hassan (2011b) and Chowdhury and Hassan (2013, 2015). Finally, we evaluated the ADI maps obtained in second step against ground-based calculations of SPI values (a drought indicator) at 19 agro-climate stations within our study area (see Fig. 1 for details). Note that we selected SPI to evaluate our results due to its simplicity and robustness in characterizing drought conditions and its flexibility to be calculated for different time periods (Wu and Wilhite, 2004; Brown, 2008; Logan et al., 2010).

2 Materials and methods
2.1 Study area

In this study, we selected the rainfed agricultural land located in the northwestern part of Jordan, Middle East, as our study area (see Fig. 1). The area is about 3522 km2 covering approximately 4% of the country’ s territory and located between 31° 41'N to 33° 30'N and 34° 19'E to 35° 59'E. Topographically, the study area has a complex terrain with elevations ranging between 600 and 1100 m a.s.l. Agriculturally, the growing season starts in October and ends in June (Saba and Al-Naber, 2010). Field crops (e.g., wheat, barley, and lentil), grasslands, rangeland, orchards (i.e., olives and fruit trees), and evergreen forests are the dominant vegetation cover/use types. Climatologically, the area is located in the semi-arid climate regions, with annual mean minimum and maximum temperatures of 11° C and 23° C, respectively. Rainy season starts in October and ends in May with more concentration in December to February. The average annual precipitation is about 457.8 mm.

Jordan is considered as one of the most drought vulnerable countries in the Middle East, and several severe drought events occurred within the last three decades and seriously affected agriculture and other economic sectors (Al-Qinna et al., 2010). For example, the 1999 drought season caused an estimation of only 1% of cereals harvested in Jordan (FAO/WFP, 1999). A five- consecutive-year drought lasting from 2003 to 2008 caused severe water shortage and severely affected agriculture production (Milton-Edwards and Hinchcliffe, 2009). Rainy season of 2013-2014 was only 52% of the long-term average annual precipitation and was described as the worst season in the last decade, leaving the dams only 43% full and the farmers in the northwestern and central regions of the country struggling to grow crops (JMWI, 2004).

Fig. 1 Map of Jordan illustrating long-term average annual precipitation isohyet distribution (a); major land use/cover map in the study area available from Jordan Ministry of Agriculture and locations of the agro-climate stations used in this study (b).

2.2 Data collection and processing

Landsat-8 and MODIS data were obtained from the U.S. Geological Survey (USGS) and the National Aeronautics and Space Administration (NASA) during the growing seasons 2013-2015 (i.e., spanning from October to June), and they were described in Table 1. It should be noted that 9 (nine) and 7 (seven) images were found to be cloud-free for the Landsat-8 data over the 2013-2014 and 2014-2015 growing seasons, respectively.

Table 1 Description of Landsat-8 and MODIS data used in this study

We used the following steps to produce Landsat-8 LST images as described by Hazaymeh and Hassan (2015b). Firstly, we transformed the original digital number (DN)-values of the Landsat-8 thermal infrared bands into top of atmosphere spectral radiance (r) measured in w/(m2• sr• μ m) using Equation 1. Then we converted them into at-satellite brightness temperature (Tb) measured in Kelvin using Equation 2 (USGS, 2013):

r=M×DN+A, (1)

Where, M and Aare multiplicative and additive rescaling factors, respectively; and K1 and K2 are thermal conversion constants. The values of M, A, K1 and K2 are readily available in the metadata file of each of the images. Secondly, we up-scaled the Landsat-8 Tb images to synchronize with the spatial resolution of MODIS LSTs and then determined the relationships between the up-scaled Landsat-8 Tb and MODIS LST images. Finally, we used these relationships to convert the original Landsat-8 Tb images into LST ones.

2.3 Generating the 8-day time-series of Landsat-8 data and calculating agricultural drought-related variables

Our adopted STI-FM algorithm (Hazaymeh and Hassan, 2015a, b) consisted of two steps. Firstly, we established a simple linear relationship between two consecutive 8-day composite of MODIS images (M(t1) and M(t2)), i.e.,

M(t2)=a×M(t1)+c.(3)

Where, a and c are slope and intercept, respectively. It would be possible that the Equation 3 might have 3 sets of co-efficient depending on the relationships between M(t1) and M(t2), such as: (i) M(t1)≈ M(t2) (i.e., ± 15%); (ii) M(t2)> M(t1) by 15%; and (iii) M(t2)< M(t1) by 15%. Secondly, we used the coefficient generated in the scope of Equation 3 into Equation 4 to generate synthetic Landsat-8 images (i.e., synth-L(t2)), where L(t1) is an actual image acquired by the Landsat-8 satellite at time t1.

synth-L(t2)=a×L(t1)+c.(4)

Upon generating synthetic Landsat-8 images, we created an 8-day time-series of actual and synthetic Landsat-8 images. We then calculated the following set of drought-related variables, such as NDWI (Gao, 1996), VSDI (Zhang et al., 2013), MSI (Hunt and Rock, 1989), NDVI (Sha et al., 2016), and NMDI (Chowdhury and Hassan, 2015).


VSD=1–((ρSWIR2–ρB)+(ρR–ρB)), (6)

(7)
NDVI=ρNIR–ρRρNIR+ρR, (8)
NMDI=ρNIR–(ρSWIR1–ρSWIR2)ρNIR+(ρSWIR1+ρSWIR2).(9)

Where, ρ is the surface reflectance values of blue (B), red (R), near infrared (NIR), and shortwave infrared (SWIR1 and SWIR2 centered at ~1.64 and ~2.14 µ m, respectively) bands.

Along with the above-mentioned spectral indices (i.e., NDWI, VSDI, MSI, NDVI, and NMDI) and LST, we implemented PCA to determine relatively less correlated variables. In this case, we computed co-variance matrix of the six input variables, eigenvalues, and related eigenvector matrix (Jensen, 2005). Then, we used these values to determine: (i) the percentage of total variance explained by each principal component using Equation 10 and (ii) the correlation or how each variable loads in each principal component using Equation 11.

%p=Ep×100∑Ep, (10)
Rvp=av×EpVarv.(11)

Where, %p is the total variance explained by component p; Ep, eigenvalue of component p; Rvp, correlation between variable v and component p; av, the eigenvector for variable v; and Varv, the variance of variable v in the co-variance matrix. Table 2 shows the eigenvalues, percentage of variance, and cumulative variance explained by each principal component (PC) for four Landsat-8 images acquired on 17 March 2014, 2 April 2014, 18 April 2014, and 4 May 2014. It revealed that PC1, PC2, and PC3 accounted for 65.03%-79.72%, 12.93%-29.03%, and 2.69%-3.87% of the total variance, respectively. Cumulatively, these three principal components accounted for 95.76%-96.74% of the variance in the dataset. Table 3 shows the corresponding correlations or loading values of each variable in these three major principal components (i.e., PC1, PC2, and PC3). According to the theory, the variable responsible for the highest loading might represent a particular PC of interest (Jensen, 2005; Akbar et al., 2011). For example, PC1 consisted of four variables (i.e., NDWI, MSI, NMDI, and VSDI) with relatively high negative correlations for all the four images. Among them, NDWI contributed the most in all the acquisition dates (i.e., -0.92 to -0.99) and it was thus considered as the representative variable for PC1. In the case of the PC2, LST was found to be the mostly contributed variable with negative loading (i.e., -0.87 to -0.98) and it was thus considered as the representative of PC2. For PC3, VSDI was the highest contributor with positive values (i.e., 0.45 to 0.52) in all the dataset and it was thus considered as PC3’ s representative. Based on this analysis, we considered NDWI, VSDI, and LST would be the set of relatively less correlated input variables for developing our agricultural drought monitoring indicator.

Table 2 Eigenvalues, percentage of variance, and cumulative variance explained by each principal component (PC) for four Landsat-8 images acquired during the growing season
Table 3 Degree of correlation or loading between each variable and each principal component (PC)
2.4 Ground-based precipitation data and its use in calculating SPI

In addition, we obtained historical daily precipitation records for thirty years during the period spanning from 1984 to 2015 available from the Jordanian Ministry of Water and Irrigation. Although there were 34 agro-climate stations located within the study area, we considered only 19 stations as reliable ones (see Fig. 1 for location information) because these 19 stations have more or less continuous records and are also located within 1 km buffer zone of agricultural land types.

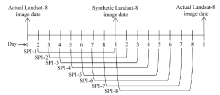
At each of the 19 stations, we used the station-specific precipitation data for calculating 8-day SPI-values using the protocols described in McKee et al. (1993). As per protocols, the SPI at a given station was calculated by considering long-term precipitation regimes over the period spanning from 1984 to 2015. The calculated SPI values were affirmed to Gamma probability distribution function and the resulted probability distribution was then converted into a Gaussian distribution to ensure that the station-specific average SPI-value over the given period would be zero (Mckee et al., 1993). The rationale of computing 8-day SPI-values was to synchronize with the 8-day intervals of the Landsat-8 actual/synthetic images. Also, note that we computed a set of 8-day SPI-values (i.e., SPI-1, SPI-2, SPI-3, SPI-4, SPI-5, SPI-6, SPI-7, and SPI-8) coinciding with each of the Landsat-8 image dates (see Fig. 2 for details). In fact, use of short-term SPI-values (e.g., daily, weekly, 10 days, and bi-weekly intervals) for agricultural drought monitoring was abundantly detailed in the literature. For example: (i) Svoboda et al. (2002), Wu and Wilhite (2004), and Brown et al. (2013) used weekly SPI-values over several states in USA; (ii) Brown (2008) used 10-day SPI values over Africa; (iii) Sims et al. (2002) compared SPI against PDSI at daily, weekly and bi-weekly temporal scales over North Carolina, USA. In general, short-term SPI-values would be required in comprehending drought conditions over agricultural land cover as crops would respond to water stress at relatively shorter time scale (McKee et al., 1993; Wu and Wilhite, 2004). On the other hand, the short-term SPI would potentially be abnormal in case of insufficient precipitation (i.e., available moisture to crops) during the period of calculation (Wu et al., 2007).

We then categorized these SPI-values into four classes upon modifying the schema described in Lloyd-Hughes and Saunders (2002) as follows: (i) wet (i.e., SPI-value> 0); (ii) mild drought (i.e., -0.99≤ SPI-value< 0); (iii) moderate drought (i.e., -1.49≤ SPI-value< -1.00); and (iv) severe drought (i.e., SPI-value≤ -1.50). Lloyd-Hughes and Saunders (2002) proposed four classes in describing wet conditions. However, we grouped all of them into one class (i.e., wet: SPI-value> 0) as detailed analyses of the wetness conditions were beyond the scope of this paper.

Fig. 2 Schematic diagram illustrating the ways of calculating 8-day SPI-values around the Landsat-8 actual/synthetic image dates

2.5 Developing a remote sensing-based agricultural drought indicator (ADI)

Over the agricultural land cover (see Fig. 1b), we extracted the set of relatively less correlated variables (i.e., NDWIi, VSDIi, and LSTi) for each of the 8-day periods (i); and then calculated the study area-specific average values for the variable of interests over each 8-day period. We then compared the instantaneous values for the variable of interest (i.e., NDWIi, VSDIi, and LSTi) against the area-specific average values for the variable of interests and defined as either “ dry” or “ wet” conditions. Such definition of dry and wet conditions was based on the natural response for the variable of interest in the context of drought. For instance: (i) the pixel would be classified as “ dry” as low values of NDWI and VSDI would indicate more dry conditions, or vice-versa; and (ii) the pixel would be classified as “ dry” as high values of LST would indicate more dry conditions, or vice-versa.

Finally, we combined the binary agricultural drought maps resulted from each of the individual variables and integrated into the following 4 classes as part of the proposed “ agricultural drought indicator” : (i) “ severe drought” if all three variables indicated “ dry” conditions; (ii) “ moderate drought” if any two variables indicated “ dry” conditions; (iii) “ mild drought” if one variable indicated “ dry” conditions; and (iv) “ wet” if all the variables indicated “ wet” conditions.

Upon generating the agricultural drought indicator maps at 8-day intervals, we evaluated them against the set of 8-day SPI-values shown in Figure 2. At the location of each of the 19 agro-climate stations where the SPI-values were calculated, we created a 1-km buffer zone and then computed the dominant (i.e., majority of occurrences) drought class within each buffer zone from the drought maps. Subsequently, we compared these drought classes with corresponding point-based SPI-values (i.e., SPI-1, SPI-2, …, SPI-8) by generating confusion matrices. We, then, used the confusion matrices to compute agreements between the remote sensing-based ADI maps and ground-based SPI-values.

3 Results and discussion

Table 4 shows the agreements between the remote sensing-derived ADI-classes and corresponding point-based SPI values (i.e., SPI-1, SPI-2, …, SPI-8). We observed higher degrees of agreements between the remote sensing-derived ADI classes and (i) SPI-4 (i.e., overall accuracy 83% and Kappa-value 76%), and (ii) SPI-5 (i.e., overall accuracy 85% and Kappa-value 78%). The observed high degrees of agreements were related to the fact that both SPI-4 and SPI-5 values were calculated and compared with the remote sensing-derived ADI values that were generated almost in the middle of the 8-day time period.

Table 4 Agreements between remote sensing-derived agricultural drought indicator classes and corresponding point-based SPI-values

In addition, we also calculated the user’ s accuracy and producer’ s accuracy for each confusion matrix to measure how well each individual class agreed with the SPI classes and the example cases (i.e., ADI vs. SPI-4 and ADI vs. SPI-5) are presented in Table 5. In both cases, we found that the drought class-specific user’ s and producer’ s accuracies were in the range 67%-93% and 62%-97%, respectively. Our findings would, in fact, support the effectiveness of our method in monitoring agricultural drought conditions at reasonably high spatial resolution (i.e., 30 m) and short time periods (i.e., 8-day). However, we observed some percentage of disagreement between remote sensing-derived ADI and SPI; which might be related to soil moisture (van Wesemael et al., 2003), and vegetation type and their growth stages (Boken et al., 2005). It would be worthwhile to mention that our proposed method had shown to forecast drought over short time period (e.g., 3 to 4 days) if no rainfall would occur.

Table 5 Examples of confusion matrices between remote sensing-derived agricultural drought indicator (ADI) and SPI classes, i.e., (a) ADI vs. SPI-4 and (b) ADI vs. SPI-5

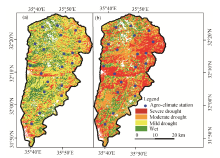
Fig. 3 Example cases of remote sensing-derived agricultural drought maps upon combining three relatively less correlated variables (i.e., NDWI, VSDI, and LST) based on: (a) actual Landsat-8 data acquired on 13 February 2014 coinciding with the period of vegetation germination; and (b) synthetic Landsat-8 data generated on 10 April 2014 at the peak period of the vegetation growth. Note that the white colored areas represented non-agricultural lands.

In order to comprehend the spatial dynamic of agricultural drought conditions, we generated agricultural drought distribution maps for each time period during the growing seasons of interest; and such example cases are shown in Figures 3a and b. Figure 3a shows agricultural drought map generated by combining the three relatively less correlated variables (i.e., NDWI, VSDI, and LST) derived from actual Landsat-8 image acquired on 13 February 2014 (i.e., during the period of vegetation germination (Saba and Al-Naber, 2010)). It showed that approximately 60% of the study area fell under the three drought classes (i.e., 28% mild drought, 14% moderate drought, and 18% severe drought). In another case as shown in Figure 3b, we combined the synthetic Landsat-8 data on 10 April 2014 (i.e., during the peak period of vegetation growth (Saba and Al-Naber, 2010)). It showed that approximately 79% of the study area fell under the three drought classes (i.e., 19% mild drought, 29% moderate drought, and 31% severe drought).

4 Conclusions

In this study, we developed a simple remote sensing-based method, namely agricultural drought indicator (ADI), for monitoring agricultural drought conditions and evaluated its applicability over a heterogeneous agriculture-dominant semi-arid region in Jordan. The ADI employed time series of relatively less correlated remote sensing-derived agricultural drought related variables (i.e., NDWI, VSDI, and LST) that were generated from actual and synthetic Landsat-8 like data at 8-day intervals and 30 m spatial resolution. Results showed higher degrees of agreement between the remote sensing-derived ADI classes and: (i) SPI-4 (i.e., overall accuracy 83% and Kappa-values 76%), and (ii) SPI-5 (i.e., overall accuracy 85% and Kappa-values 78%). It is our sincere hope that our method would provide better understanding and more comprehensive view of agricultural drought conditions and that our method can in turn help us in mitigating its severe consequences and enhancing agricultural and water management practices. Despite the strong performance of our proposed remote sensing-derived ADI, we would like to mention the following issues for potential improvements. First, other factors, such as topography, soil properties, land use/cover, vegetation phenology, and agricultural management practices, would be worthwhile to investigate as they might play significant role in agricultural drought conditions and levels. Second, we strongly recommend using other ground-based drought related information, such as temperature and evapotranspiration besides using ground-based precipitation data. Third, we strongly recommend the method to be thoroughly evaluated prior any implementation in environments other than semi-arid ones.

Acknowledgements

We would like to thank the University of Calgary, Canada and Yarmouk University, Jordan for providing partial financial support in the form of awards to Mr. Khaled HAZAYMEH and the National Sciences and Engineering Research Council (NSERC), Canada for a Discovery grant to Dr. Quazi HASSAN. We would also like to thank USGS, NASA, and the Jordanian Ministry of Water and Irrigation for providing the required data at no cost.

The authors have declared that no competing interests exist.

Reference
[1] AghaKouchak A, Farahmand A, Melton F S, et al. 2015. Remote sensing of drought: progress, challenges and opportunities. Reviews of Geophysics, 53(2): 452-480. [Cited Within:1]
[2] Akbar T A, Hassan Q K, Achari G. 2011. A methodology for clustering lakes in Alberta on the basis of water quality parameters. Clean-Soil, Air, Water, 39(10): 916-924. [Cited Within:2]
[3] Akther M S, Hassan Q K. 2011 a. Remote sensing based estimates of surface wetness conditions and growing degree days over northern Alberta, Canada. Boreal Environment Research, 16(5): 407-416. [Cited Within:1]
[4] Akther M S, Hassan Q K. 2011 b. Remote sensing-based assessment of fire danger conditions over boreal forest. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 4(4): 992-999. [Cited Within:2]
[5] Al-Qinna M I, Hammouri N A, Obeidat M M, et al. 2010. Drought analysis in Jordan under current and future climates. Climatic Change, 106(3): 421-440. [Cited Within:1]
[6] Anderson M C, Hain C, Wardlow B, et al. 2011. Evaluation of drought indices based on thermal remote sensing of evapotranspiration over the Continental United States. Journal of Climate, 24(8): 2025-2044. [Cited Within:1]
[7] Anjum S A, Xie X, Wang L, et al. 2011. Morphological, physiological and biochemical responses of plants to drought stress. African Journal of Agricultural Research, 6(9): 2026-2032. [Cited Within:1]
[8] Benmecheta A, Abdellaoui A, Hamou A. 2013. A comparative study of land surface temperature retrieval methods from remote sensing data. Canadian Journal of Remote Sensing, 39(1): 59-73. [Cited Within:1]
[9] Boken V K, Cracknell A P, Heathcote R L. 2005. Monitoring and Predicting Agricultural Drought: A Global Study. New York: Oxford University Press, 472. [Cited Within:1]
[10] Brown J F, Wardlow B D, Tadesse T, et al. 2013. The vegetation drought response index (VegDRI): a new integrated approach for monitoring drought stress in vegetation. GIScience & Remote Sensing, 45(1): 16-46. [Cited Within:1]
[11] Brown L, Chen J M, Leblanc S G, et al. 2000. A shortwave infrared modification to the simple ratio for LAI retrieval in boreal forests: an image and model analysis. Remote Sensing of Environment, 71(1): 16-25. [Cited Within:1]
[12] Brown M E. 2008. Derived agricultural and climate monitoring products. In: Brown M E, ed. Famine Early Warning Systems and Remote Sensing Data. Berlin: Springer-Verlag, 83-96. [Cited Within:1]
[13] Chakraborty A, Sehgal V K. 2010. Assessment of agricultural drought using MODIS derived normalized difference water index. Journal of Agricultural Physics, 10: 28-36. [Cited Within:1]
[14] Chowdhury E H, Hassan Q K. 2013. Use of remote sensing-derived variables in developing a forest fire danger forecasting system. Natural Hazards, 67(2): 321-334. [Cited Within:2]
[15] Chowdhury E H, Hassan Q K. 2015. Development of a new daily-scale forest fire danger forecasting system using remote sensing data. Remote Sensing, 7(3): 2431-2448. [Cited Within:4]
[16] FAO/WFP. 1999. FAO/WFP Crop and Food Supply Assessment Mission to the Kingdom of Jordan. Rome: FAO. [2015-12-16]. http://www.fao.org/docrep/004/x2207e/x2207e00.htm#P176_17001. [Cited Within:1]
[17] Gao B C. 1996. NDWI-a normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sensing of Environment, 58(3): 257-266. [Cited Within:3]
[18] Ghulam A, Li Z L, Qin Q M, et al. 2008. Estimating crop water stress with ETM+ NIR and SWIR data. Agricultural and Forest Meteorology, 148(11): 1679-1695. [Cited Within:1]
[19] Gu Y, Hunt E, Wardlow B, et al. 2008. Evaluation of MODIS NDVI and NDWI for vegetation drought monitoring using Oklahoma Mesonet soil moisture data. Geophysical Research Letters, 35(22): L22401, doi: DOI:10.1029/2008GL035772. [Cited Within:1]
[20] Hao Z C, AghaKouchak A, Nakhjiri N, et al. 2014. Global integrated drought monitoring and prediction system. Scientific Data, 1: 140001. [Cited Within:1]
[21] Hao Z H, AghaKouchak A. 2013. Multivariate stand ardized drought index: a parametric multi-index model. Advances in Water Resources, 57: 12-18. [Cited Within:1]
[22] Hazaymeh K, Hassan Q K. 2015 a. Fusion of MODIS and Land sat-8 surface temperature images: a new approach. PLoS One, 10(3): e0117755. [Cited Within:1]
[23] Hazaymeh K, Hassan Q K. 2015 b. Spatiotemporal image-fusion model for enhancing the temporal resolution of Land sat-8 surface reflectance images using MODIS images. Journal of Applied Remote Sensing, 9(1): 096095. [Cited Within:1]
[24] Hazaymeh K, Hassan Q K. 2016. Remote sensing of agricultural drought monitoring: a state of art review. Aims Environmental Science, 3(4): 604-630. [Cited Within:1]
[25] Hunt E R Jr, Rock B N. 1989. Detection of changes in leaf water content using near-and middle-infrared reflectances. Remote Sensing of Environment, 30(1): 43-54. [Cited Within:2]
[26] Jackson R D, Idso S B, Reginato R J, et al. 1981. Canopy temperature as a crop water stress indicator. Water Resources Research, 17(4): 1133-1138. [Cited Within:1]
[27] Jang J D, Viau A A, Anctil F. 2006. Thermal-water stress index from satellite images. International Journal of Remote Sensing, 27(8): 1619-1639. [Cited Within:1]
[28] Jensen J R. 2005. Introductory Digital Image Processing: A Remote Sensing Perspective (3rd ed. ). New Jersey: Prentice Hall, 526. [Cited Within:4]
[29] JMWI (Jordanian Ministry of Water and Irrigation). 2014. [2015-12-16]. http: //mwi. gov. jo/sites/ar-jo/Lists/List1/DispForm.
1)aspx?ID=196. (in Arabic) [Cited Within:1]
[30] Kogan F. 2002. World droughts in the new millennium from AVHRR-based vegetation health indices. EOS, Transactions American Geophysical Union, 83(48): 557-563. [Cited Within:2]
[31] Lambin E F, Ehrlich D. 1996. The surface temperature-vegetation index space for land cover and land -cover change analysis. International Journal of Remote Sensing, 17(3): 463-487. [Cited Within:1]
[32] Li J, Heap A D. 2014. Spatial interpolation methods applied in the environmental sciences: a review. Environmental Modelling & Software, 53: 173-189. [Cited Within:1]
[33] Lloyd-Hughes B, Saunders M A. 2002. A drought climatology for Europe. International Journal of Climatology, 22(13): 1571-1592. [Cited Within:1]
[34] Logan K E, Brunsell N A, Jones A R, et al. 2010. Assessing spatiotemporal variability of drought in the U. S. central plains. Journal of Arid Environments, 74(2): 247-255. [Cited Within:1]
[35] McKee T B, Doesken N J, Kleist J. 1993. The relationship of drought frequency and duration to time scales. In: Proceedings of the 8th Conference on Applied Climatology. Anaheim, California: Conference on Applied Climatology, 179-184. [Cited Within:3]
[36] McVicar T R, Jupp D L B. 1998. The current and potential operational uses of remote sensing to aid decisions on drought exceptional circumstances in Australia: a review. Agricultural Systems, 57(3): 399-468. [Cited Within:1]
[37] Milton-Edwards B, Hinchcliffe P. 2009. Jordan: A Hashemite Legacy (2nd ed. ). New York: Routledge, 147. [Cited Within:1]
[38] Palmer W C. 1965. Meteorological Drought. Washington D. C. : U. S. Weather Bureau, Research Paper No. 45: 58. [Cited Within:1]
[39] Palmer W C. 1968. Keeping track of crop moisture conditions, nationwide: the new crop moisture index. Weatherwise, 21(4): 156-161. [Cited Within:1]
[40] Ranjan R, Sahoo R N, Chopra U K, et al. 2015. Assessment of water status in wheat (Triticum aestivum L. ) using ground based hyperspectral reflectance. In: Proceedings of the National Academy of Sciences, India Section B: Biological Sciences . India: Springer, 1-12, doi: DOI:10.1007/s40011-015-0618-6. [Cited Within:1]
[41] Saba M, Al-Naber G. 2010Analysis of Jordan vegetation cover dynamics using MODIS/NDVI from 2000 to 2009. In: Proceedings of the International Conference of Food Security and Climate Change in Dry Areas. Amman: International Center for Agricultural Research in the Dry Areas (ICARDA). [Cited Within:2]
[42] Samanta A, Ganguly S, Myneni R B. 2011. MODIS enhanced vegetation index data do not show greening of amazon forests during the 2005 drought. New Phytologist, 189(1): 11-15, doi: DOI:10.1111/j.1469-8137.2010.03516.x. [Cited Within:1]
[43] Sand holt I, Rasmussen K, Andersen J. 2002. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sensing of Environment, 79(2-3): 213-224. [Cited Within:2]
[44] Sha Z Y, Zhong J L, Bai Y F, et al. 2016. Spatio-temporal patterns of satellite-derived grassland vegetation phenology from 1998 to 2012 in Inner Mongolia, China. Journal of Arid Land , 8(3): 462-477. [Cited Within:1]
[45] Shahabfar A, Ghulam A, Eitzinger J. 2012. Drought monitoring in Iran using the perpendicular drought indices. International Journal of Applied Earth Observation and Geoinformation, 18: 119-127. [Cited Within:1]
[46] Sims A P, Niyogi D D S, Raman S. 2002. Adopting drought indices for estimating soil moisture: a North Carolina case study. Geophysical Research Letters, 29(8): 1183. [Cited Within:1]
[47] Svoboda M, LeComte D, Hayes M, et al. 2002. The drought monitor. Bulletin of the American Meteorological Society, 83: 1181-1190. [Cited Within:1]
[48] Tucker C J, Choudhury B J. 1987. Satellite remote sensing of drought conditions. Remote Sensing of Environment, 23(2): 243-251. [Cited Within:1]
[49] USGS. 2013. Using the USGS Land sat 8 product. USA: USGS. [2015-12-16]. http://landsat.usgs.gov/Landsat8_Using_Product.php. [Cited Within:1]
[50] van Wesemael B, Cammeraat E, Mulligan M, et al. 2003. The impact of soil properties and topography on drought vulnerability of rainfed cropping systems in southern Spain. Agriculture, Ecosystems & Environment, 94(1): 1-15. [Cited Within:1]
[51] Wang W, Huang D, Wang X G, et al. 2011. Estimation of soil moisture using trapezoidal relationship between remotely sensed land surface temperature and vegetation index. Hydrology and Earth System Sciences, 15(5): 1699-1712. [Cited Within:1]
[52] Wilhite D A, Svoboda M D, Hayes M J. 2007. Understand ing the complex impacts of drought: a key to enhancing drought mitigation and preparedness. Water Resources Management, 21(5): 763-774. [Cited Within:1]
[53] Wu H, Wilhite D A. 2004. An operational agricultural drought risk assessment model for Nebraska, USA. Natural Hazards, 33(1): 1-21. [Cited Within:3]
[54] Wu H, Svoboda M D, Hayes M J, et al. 2007. Appropriate application of the stand ardized precipitation index in arid locations and dry seasons. International Journal of Climatology, 27(1): 65-79. [Cited Within:1]
[55] Wu J J, Zhou L, Liu M, et al. 2013. Establishing and assessing the integrated surface drought index (ISDI) for agricultural drought monitoring in mid-eastern China. International Journal of Applied Earth Observation and Geoinformation, 23: 397-410. [Cited Within:1]
[56] Zhang N, Hong Y, Qin Q M, et al. 2013. VSDI: a visible and shortwave infrared drought index for monitoring soil and vegetation moisture based on optical remote sensing. International Journal of Remote Sensing, 34(13): 4585-4609. [Cited Within:2]
[57] Zhou L, Lyu A. 2016. Investigating natural drivers of vegetation coverage variation using MODIS imagery in Qinghai, China. Journal of Arid Land , 8(1): 109-124. [Cited Within:1]
[58] Zhu G L, Ju W M, Chen J M, et al. 2014. A novel moisture adjusted vegetation index (MAVI) to reduce background reflectance and topographical effects on LAI retrieval. PLoS ONE, 9(7): e102560. [Cited Within:1]