The experiments were conducted from March to July in both 2015 and 2016 in a solar greenhouse at the Experimental Station of Farmland Irrigation Research, Institute of Chinese Academy of Agricultural Sciences (35° 09′ N, 113° 47′ E; 78.7 m a.s.l.), Xinxiang City, Henan Province, China. The annual precipitation and potential evaporation in the station were 548 and 1908 mm, respectively, with an annual mean air temperature of 14° C, sunshine duration of 2398 h, and frost-free days of 200 d. The solar greenhouse was made by a steel frame with a covering area of 510 m² (60 m× 8.5 m) and covered by a 0.2-mm thick non-drop polyethylene sheet. The roof of the greenhouse was cotton-quilts with 2.5-cm thick cotton wadding, and the heat-insulating materials were mounted in the back wall to maintain interior temperature. The greenhouse was equipped with a ventilation system to adjust its temperature and humidity. The soil used in the experiment was loam, with a mean bulk density of 1.51 g/cm³, field capacity of 0.366 cm³/cm³ and wilting-point water content of 0.09 cm³/cm³ in the depth of 0-90 cm.

Tomato (Lycopersicon esculentumMill. cv. Jingding) was planted in 18 plots. Each plot was 8.8 m² (8.0 m× 1.1 m) with 50 plants planted in two rows. The distance between the two rows alternated from 65 to 45 cm in the 18 plots. The plants were watered by drip irrigation and the spatial interval of the emitters in each drip tape was 33 cm. The designed discharge rate of each drip tape was 1.1 L/h. The irrigation frequencies were determined based on the cumulative evaporation (E_p) measured from a pan of 20 cm in diameter placed 30 cm above the canopy at the center of the greenhouse. When E_p reached to 20 (± 2) mm, irrigation started and the plant-pan coefficient of 0.9 was used in this experiment (Liu et al., 2013). Therefore, the amount of applied irrigation water can be calculated by the equation I_r=0.9× E_p, where E_p is the cumulative evaporation from 20 cm diameter pan (mm). To ensure seeding growth, we irrigated 20 mm of water to all plots just after the transplanting. The plants were irrigated 14 times in each of the two seasons, and the total irrigation amount was 282.4 mm in 2015 and 280.7 mm in 2016. During the experiments, we adopted a method similar to that used by local farmers to maintain the greenhouses, including fertilization application, pollination, and pest control.

2.3.1 Evapotranspiration measurements

Evapotranspiration (ET) of the tomato was measured using sap flow system combined with micro-lysimeters in 2015 and with weighing lysimeters in 2016.

Soil evaporation was measured daily from a micro-lysimeters from 17 March to 15 July, 2015. The micro-lysimeter was made from galvanized iron, consisting of an inner cylinder and an outer cylinder. The diameters of the inner and outer cylinders were 10 and 12 cm, respectively, and its height was 15 cm. For easy operation without physically disturbing the soil, the outer tank was fixed into the soil with its top level with the soil surface. The inner cylinder was then pushed into the soil until its top was leveled with the soil surface. The base of the micro-lysimeter was sealed by a plastic foil to avoid percolation. The inner cylinder was weighted daily at 08:00 using an electronic balance with a precision of 0.1 g, and the soil evaporation was defined as the difference between two consecutive weights. To ensure the accuracy, we replaced the soil in the inner tank every two days or after irrigation. In each of six randomly selected plots, these micro-lysimeters were installed between two neighboring plants in the same row as well as between two neighboring plants in two different rows, respectively, each having two replicates.

A sap flow system (Flow32-1k system, Dynamax, Houston, TX, USA) was used to measure the transpiration. In each plot, the SGA-WS gauges of the sap flow (DYNAMAX Inc., USA) were installed at representative plants of the tomatoes. Eight health plants were randomly selected and their stem diameters were measured prior to installing the gauges. The measured stem diameters varied from 9.0 to 12.0 mm. Therefore, the SGA9-WS/SGA10-WS and SGB12-WS gauges were used to measure the sap flow. The gauges were fixed on the stems 20 cm above the ground surface to avoid the effect of surface heat flux (Qiu et al., 2015). The details of the installation and measurements of the sap flow system can be found in Gao et al. (2013). Sap flow from 15 May to 15 July, 2015 was measured, in which the sap flow data were collected after every 15 min by a CR-1000 data logger (Campbell Scientific Inc., USA). The sap flow of each individual plant was then converted to plant transpiration using the following formula (Ham et al., 1990):

$$T=\frac{1}{1000}\bigg[\sum^n_{i=1}\frac{f_i/LA_i}{n}\bigg]LAI, \ \ (1)$$

where, T is the plant transpiration after normalizing the sap flow data by the leaf area (mm/h); f_i, the stem flow (g/h); LA_i, the leaf area (m²); n, the number of plants measured; and LAI, the leaf area index (m²/m²).

ET was measured by two weighing lysimeters (1.0 m long, 1.0 m wide and 1.2 m deep) located in the center of the plots from 9 March to 10 July, 2016. The weighing lysimeter can measure up to 2.5 tons with a precision of 0.01 mm, and the data were collected after every 60 min by a microcomputer. The planting pattern in the weighing lysimeter was the same as the outside. There were six health plants in each weighing lysimeter. To avoid interferences with plants outside, we popped up all the six plants by bamboo sticks.

2.3.2 Soil water content and leaf area index

Soil water content was measured using the ECH₂O soil moisture monitoring system. Five ECH₂O soil moisture probes were placed at depths of 10, 20, 30, 40, and 60 cm, respectively. The soil water content data were collected after each 30 min using the EM50 data logger (Decagon Devices Inc., USA).

The leaf area was measured manually at an interval of 5-10 days. Thirty plants were sampled at the center of each plot. The leaf length (L) and the greatest leaf width (W_m) were measured with a ruler, and the conversion coefficient of 0.64 for the leaf area was obtained from fitting the measured results to that drawn using CAD software (Liu et al., 2009). LAI was calculated as follows:

$$LAI=\frac{\sum^n_{i=1}(L\times W_m\times 0.64)_i}{S_R\times S_p}, \ \ (2)$$

where, S_R (55 cm) is the average row space, and S_p (33 cm) is the average distance between two neighboring plants.

2.3.3 Leaf stomatal resistance

The leaf stomatal resistance was directly measured using a porometer (SC-1, Decagon Devices Inc., USA) at an interval of 7-10 days. In each plot, 6-9 functional leaves of healthy plants were randomly selected. Diurnal variations of the leaf stomatal resistance were measured at seedling, flowering-fruit bearing, full fruit, and picking stages.

2.3.4 Meteorological data

The solar radiation (R_s), net radiation (R_n), relative humidity (RH), air temperature (T_a) and wind speed (u) were measured using an automatic weather station installed 2.0 m above the ground surface. The R_s was measured by a radiometer (LI200X, Campbell Scientific Inc., USA) with sensitivity of 0.2 kW/(m²• mV), and the R_n was measured by a net radiometer (NR LITE2, Kipp & Zonen, Delft, Netherlands) with sensitivity of 10 μ V/(W• m²). The T_a and RH were measured by a temperature and relative humidity recorder (CS215, Campbell Scientific Inc., USA). The u was recorded by an air velocity meter (Wind Sonic, Gill, UK) with an accuracy of ± 0.02 m/s. The surface temperature (T_s) was measured using an infrared radiation pyrometer (SI-111, Campbell Scientific Inc., USA) with an accuracy of ± 0.2° C, which is mounted 30 cm above the canopy with its sensor approximately 45° to the horizon of the canopy pointing northward. The soil heat flux (G) was measured at two points, one between two plants in a row and the other between two rows, using the heat flux plates (HFP01, Hukseflux, Netherlands) with sensitivity of 50 µ V/(W• m²), installed 5 cm below the ground surface. All measurements were collected after each 10 s, and the averages over 30 min were calculated and the results were stored in a CR-1000 data logger (Campbell Scientific Inc., USA). The maximum, minimum, and mean of daily averages of all meteorological parameters measured in 2015 and 2016 are shown in Table 1.

Table 1

Table 1

Table 1 The maximum, minimum and mean of daily averages of meteorological data measured in 2015 and 2016 Year Statistic Rs (W/m2) Rn (W/m2) Ta (° C) Ts (° C) VPD (kPa) RH (%) u (m/s) 2015 Maximum 231.14 172.57 31.33 29.09 2.46 99.78 0.43 Minimum 25.17 16.19 15.41 15.87 0.02 47.86 0.06 Mean 136.96 94.64 24.30 23.10 0.77 82.06 0.14 2016 Maximum 207.09 175.32 31.75 29.06 1.95 99.39 0.34 Minimum 8.60 3.08 11.40 14.62 0.02 52.24 0.05 Mean 128.12 98.40 22.93 22.21 0.73 74.86 0.15 Note: Rs, solar radiation; Rn, net radiation; Ta, air temperature; Ts, surface temperature; VPD, water vapor pressure deficit; RH, relative humidity; u, wind speed.

Table 1 The maximum, minimum and mean of daily averages of meteorological data measured in 2015 and 2016

The Penman-Monteith (PM) model for estimating ET is described as follows (Monteith, 1965):

(3)

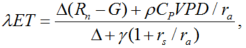
where, λ is the latent heat of water vaporization (J/kg); ET, the evapotranspiration rate; Δ , the slope of saturation water vapor pressure-temperature curve (kPa/K); R_n, the net radiation (W/m²); G, soil heat flux (W/m²); C_p, the specific heat of dry air at a constant pressure (J/(kg• K)); ρ , the air density (kg/m³); VPD, the water vapor pressure deficit (KPa); r_a, the aerodynamic resistance (s/m); γ , the psychometric constant (KPa/K); and r_s, the surface resistance (s/m).

We developed a surface resistance model according to the resistance law of fluid transmission, canopy resistance, and soil resistance. From the principle of parallel electric circuit, the model can be described as follows:

(4)

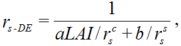
where, r_s-DE is the developed surface resistance (s/m); \(r^c_s\), the canopy resistance (s/m); \(r^s_s\), the soil resistance (s/m); LAI, the leaf area index; and a and b are the empirical coefficients which can be obtained by least-square fitting of the measurements from the weighing lysimeter in 2016. In our study, the values of a and b were 1.52 and 0.05, respectively, and the canopy resistance was estimated by the stomatal resistance as follows:

(5)

where, r_sT is the stomatal resistance (s/m) and can be obtained from its relationship with the solar radiation. The effective leaf area index, LAI_e, can be set as follows: LAI_e equals to LAI when LAI≤ 2, equals to 2 when 2< LAI< 4, and equals to LAI/2 when LAI≥ 4 (Gardiol et al., 2003).

The soil resistance (\(r^s_s\)) was calculated using the Anadranistakis model as follows (Anadranistakis et al., 2000):

(6)

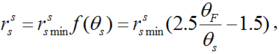
where, \(r^s_s min\) is the minimum soil resistance when soil water content is at field capacity, taken as 100 s/m in this paper (Camillo and Gurney, 1986); θ _F, the field capacity for soil in depth of 0-10 cm; and θ _s, the soil water content in depth of 0-10 cm.

The aerodynamic resistance was calculated by three methods. The first one is from Perrier (1975a, b) and can be described as follows:

(7)

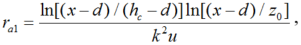
where, k is the Karman constant (0.40); x, the reference height (2 m); h_c, the mean crop height (m); d, the zero plane displacement (m); u, the wind speed at the reference height (m/s); and z₀, the roughness length of the crop relative to momentum transfer (m). The z₀ and d are defined as functions of crop height and LAI(Brenner and Incoll, 1997) as follows:<

$$d=1.1h_cln(1+X{0.25}), \ \ (8)$$

(9)

where, X=c_d× LAI with c_d being the mean drag coefficient and taken as 0.07 (Brenner and Incoll, 1997), and z₀' is the roughness length of bare soil surface (0.01 m) (Shuttleworth and Wallace, 1985).

Considering that wind speed in solar greenhouse is generally small under natural ventilation and that the aerodynamic resistance could become infinite when wind speed is close to zero, the second method for calculating the aerodynamic resistance from the formula of Thom and Oliver (1977) is adopted:

(10)

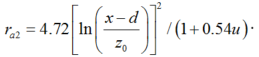
When wind speed is negligible, r_a2 reduces to

(11)

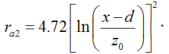
The above methods were also used by Chen et al. (2007) and Liu et al. (2011) to calculate the aerodynamic resistance in solar greenhouse.

Since eddy diffusion can transport both air and water vapor, the aerodynamic resistance (r_a3) calculated method is to use the convective heat transfer coefficient for individual leaf as follows (Zhang and Lemeur, 1992):

(12)

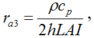
where, h is the convective heat transfer coefficient (W/(m²• K)). Qiu et al. (2013) showed that the convection in greenhouses was dominated by mixed convection during daytime and h can hence be calculated as follows (Stanghellini, 1993):

(13)

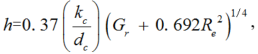
where, k_c is the thermal conductivity of air (W/(m• K)); d_c, the characteristic dimension of the leaf (m); G_r, the Grashof number; and R_e, the Reynolds number. d_c can be calculated as follows (Montero et al., 2001):

(14)

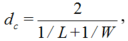
where, L is the leaf length (m) and W is the leaf width (m). The G_r and R_e in Equation 13 can be calculated as follows (Bailey et al., 1993):

(15)

(16)

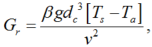
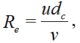
where, β is the thermal expansion coefficient of air (taken as 3.315× 10^-3/K); g, the gravity acceleration (m/s²); and v, the kinematic viscosity of air (taken as 16.4× 10^-6 m²/s).

The accuracy of the models was quantified by the coefficient of determination (R²). The mean absolute error (MAE), the root mean square error (RMSE) and the index of agreement (d_l) can be expressed as follows (Mayer and Butler, 1993):

(17)

(18)

(19)

(20)

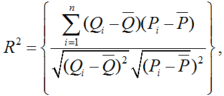
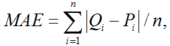
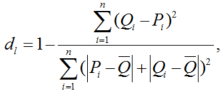
where, P_i and Q_i are the calculated and measured values, respectively; \(\overline{Q}\), the mean of the measurements; \(\overline{P}\), the mean of the calculations; and n, the number of measurements.

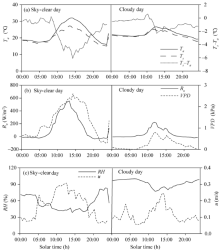
The diurnal variations of Ta, Ts, T_s-T_a, Rn, VPD, RH, and u in a typical sky-clear day (20 May, 2015) and a cloudy day (29 May, 2015) are shown in Figure 1. There was no remarkable difference between T_s and T_a before 09:00 in the sky-clear day and before 11:00 in the cloudy day. During the rest time of the same day, T_s was consistently lower than T_a (Fig. 1a). The mean maximum difference between T_s and T_a occurred around 14:00, reaching 6° C in the sky-clear day and 2.3° C in the cloudy day, due to high transpiration rate. Plants associated with elevated VPD and radiation make their leaves cooler than the ambient air (Rouphael and Colla, 2004; Liu and Fan, 2012).

The diurnal variations of R_n and VPD were similar (Fig. 1b). The R_n and VPD peaked around 14:00 in the sky-clear day, reaching 554.2 W/m² and 2.6 kPa, respectively, while in the cloudy day they peaked at 11:30, reaching 224.2 W/m² and 0.8 kPa, respectively. The average of RH in the sky-clear day is 56.1%, lower than that in the cloudy day (92.1%). Since a part of the vents in the greenhouse was switched off in night, it results in the u in the daytime higher than that in the night (Fig. 1c).

Fig. 1

	Figure Option ViewDownloadNew Window
	Fig. 1 Diurnal variations of air temperature (Ta), surface temperature (Ts), difference between canopy and air temperatures (Ts-Ta), net radiation (Rn), water vapor pressure deficit (VPD), relative humidity (RH) and wind speed (u) measured in a typical sky-clear day (20 May, 2015) and a cloud day (29 May, 2015)

The stomatal resistance (r_sT) is an important parameter for calculating canopy resistance (\(r^c_s\)). Our statistical analysis revealed that the r_sT was a function of R_s during the daytime (Fig. 2). The relationship between r_sT and R_s can be fitted to an exponential function as follows:

$$R_{sT}=23.21exp(1021.06/R_s+365.71)).\ \ (21)$$

The value of R² was 0.82, with MAE of 17.58 s/m and RMSE of 25.10 s/m. Therefore, the stomatal resistance of the tomato in the solar greenhouse can be accurately estimated from its relationship with R_s in our study.

Fig. 2

	Figure Option ViewDownloadNew Window
	Fig. 2 An exponential relationship between leaf stomatal resistance (rsT) and solar radiation (Rs)

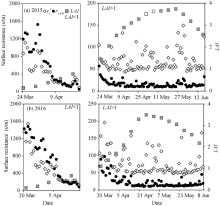
Figure 3 shows the seasonal variations of the \(r^c_s\), r_s-DE calculated by the proposed model, as well as LAI during the experiments in 2015 and 2016. The r_s-DE and \(r^c_s\) decreased rapidly as LAIincreased during the seedling period, and the r_s-DE was slightly higher than\(r^c_s\), especially when the LAI was less than 1.0. However, when the LAI was higher than 1.0, the canopy gradually covered the soil surface and the soil surface resistance decreased as a result (the mean was less than 100 s/m in our study), resulting in the r_s-DE slightly lower than the\(r^c_s\). When LAI was lower than 1.0, the means of r_s-DE and \(r^c_s\) were 632.97 and 444.87 s/m, respectively in 2015, and 738.37 and 555.72 s/m, respectively in 2016. When LAIwas higher than 1.0, the means of \(r^c_s\) were 72.3% and 68.2% higher than the means of the r_s-DE in 2015 and 2016, respectively.

Fig. 3

	Figure Option ViewDownloadNew Window
	Fig. 3 Seasonal variations of the daily canopy resistance (\(r^c_s\)), the surface resistance (rs-DE) calculated by the proposed model, and the leaf area index (LAI) in 2015 and 2016

In the solar greenhouse, the wind speed was small and the daily mean wind speed varied from 0.05 to 0.43 m/s (see Table 1). Figure 4 shows the seasonal variations of the aerodynamic resistance (r_a1, r_a2, and r_a3) calculated by the three models proposed by Perrier (1975a, b), Thom and Oliver (1977) and Zhang and Lemeur (1992), respectively, during the experiments in 2015 and 2016. The variations of r_a1, r_a2, and r_a3 were comparable and they all peaked at the seedling stage and then decreased gradually. The value of r_a1 was consistently higher than those of r_a2 and r_a3 during the experiments, while the value of r_a3 was higher than that of r_a2, especially in the seedling stage. During the seedling stage, r_a1 was mainly affected by wind speed and its value was higher than 800 s/m when wind speed was below 0.1 m/s. The r_a3 was remarkably higher than r_a2 in the seedling stage, and the means of r_a3 were 63.1% and 68.3% higher than the means of r_a2 in 2015 and 2016, respectively.

Fig. 4

	Figure Option ViewDownloadNew Window
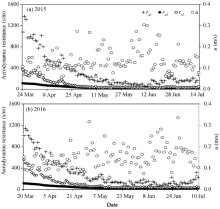	Fig. 4 Seasonal variations of the aerodynamic resistance calculated by the three methods in 2015 and 2016. ra1 from Perrier (1975a, b); ra2 from Thom and Oliver (1977); ra3 from Zhang and Lemeur (1992); u, wind speed.

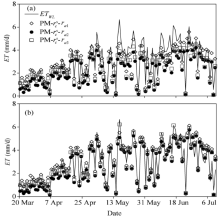
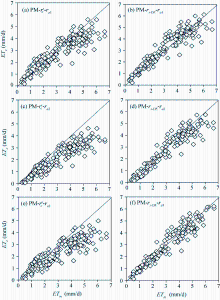
Figure 5 shows the seasonal variations of the daily ET estimated by the developed surface resistance model and the canopy resistance model combined with the aerodynamic resistance calculated by the three methods. The results measured by the weighing lysimeter in 2016 were also plotted for comparison. It can be seen from Figure 5 that the combinations of PM-\(r^c_s\)-r_a1, PM-\(r^c_s\)-r_a2, and PM-\(r^c_s\)-r_a3 underestimated the daily ETby 4.8%, 38.1% and 22.9%, respectively during the entire experimental period. In contrast, the daily ET estimated using the PM-r_s-DE-r_a3 was in good agreement with the measurements, while the PM-r_s-DE-r_a1 and PM-r_s-DE-r_a2 combinations slightly overestimated and underestimated the daily ET by 5.2% and 9.6%, respectively. To evaluate the performance of the r_s-DE model in the seedling stage, we compared the diurnal variations of the hourly ET estimated by PM-\(r^c_s\)-r_a3 and PM-r_s-DE-r_a3 with the measured ET from the weighing lysimeter (ET_WL). Figure 6 shows that the ET estimated by PM-r_s-DE-r_a3 was close to ET_WL, whereas the ET estimated by PM-\(r^c_s\)-r_a3 was higher than ET_WL, especially around lunch time, due to the difference between r_s-DE and \(r^c_s\) in treating the integrated influence of canopy and soil surface resistances as discussed above.

Fig. 5

	Figure Option ViewDownloadNew Window
	Fig. 5 Seasonal variations of the daily evapotranspiration (ET) estimated by PM model in combination with different resistance models (a). The results measured from the weighing lysimeter (ETWL) in 2016 were also plotted for comparison (b).

Fig. 6

	Figure Option ViewDownloadNew Window
	Fig. 6 Comparison between diurnal variations of the hourly evapotranspiration (ET) estimated by PM-\(r^c_s\)-ra3, PM-rs-DE-ra3 and the results measured from the weighing lysimeter (ETWL) from 25 March to 31 March, 2016

Figure 7 and Table 2 compare the daily ET estimated by the PM model using different resistance models and the measurements from the sap flow system combined with the micro-lysimeter in 2015 and with the weighing lysimeter in 2016. Table 2 reveals that the \(r^c_s\)model in combination with r_a1, r_a2, and r_a3 underestimated the daily ET in the two years, with a slope of 0.86, 0.68, and 0.73, respectively. The r_s-DE model in combination withr_a2 underestimated the daily ET by 10.5 % in the two years, with the slope, MAE and RMSE being 0.90, 0.46 mm/d and 0.60 mm/d, respectively. The r_s-DE model in combination with r_a1 and r_a3 works better: the slope being 0.98 (for r_a1) and 0.96 (for r_a3), MAE being 0.40 and 0.34 mm/d, and RMSE being 0.55 and 0.45 mm/d. However, the determination coefficient of r_a3 was superior to r_a1. These indicated that combining the aerodynamic resistance calculated from the eddy diffusion theory with the developed surface resistance can improve the PM model in estimating the daily ET of tomato in the solar greenhouse.

Fig. 7

	Figure Option ViewDownloadNew Window
	Fig. 7 Comparison between the daily evapotranspiration (ET) estimated by the PM model using different resistance models (ETc) and the results measured from the sap flow system combined with the micro-lysimeter and with the weighing lysimeter (ETm) in 2015 and 2016

Table 2

Table 2

Table 2 Comparing the daily evapotranspirations estimated by the proposed surface model and the canopy resistance model, using the three aerodynamic resistance methods, with the results measured from the sap flow system combined with the micro-lysimeter and with the weighing lysimeter in 2015 and 2016 Surface resistance Aerodynamic resistance Regression equation R2 MAE (mm/d) RMSE (mm/d) dl \(\overline{Q}\) (mm/d) \(\overline{P}\) (mm/d) N \(r^c_s\) ra1 ETc=0.86ETm 0.76 0.59 0.79 0.92 3.24 2.91 175 ra2 ETc=0.68ETm 0.85 1.02 1.23 0.83 3.24 2.23 175 ra3 ETc=0.73ETm 0.77 0.89 1.13 0.84 3.24 2.43 175 rs-DE ra1 ETc=0.98ETm 0.86 0.40 0.55 0.97 3.24 3.26 175 ra2 ETc=0.90ETm 0.90 0.46 0.60 0.96 3.24 2.90 175 ra3 ETc=0.96ETm 0.92 0.34 0.45 0.98 3.24 3.12 175 Note: ETc is the daily evapotranspiration estimated by the proposed surface model and the canopy resistance model using the three aerodynamic resistance methods, and ETm is the measurements from the sap flow system combined with the micro-lysimeter and the weighing lysimeter. \(r^c_s\), the canopy resistance; rs-DE, surface resistance; MAE, mean absolute error; RMSE, root mean square error; dl, index of agreement; \(\overline{Q}\), mean of the measurements; \(\overline{P}\), mean of the calculations; N, sampling numbers.

Table 2 Comparing the daily evapotranspirations estimated by the proposed surface model and the canopy resistance model, using the three aerodynamic resistance methods, with the results measured from the sap flow system combined with the micro-lysimeter and with the weighing lysimeter in 2015 and 2016

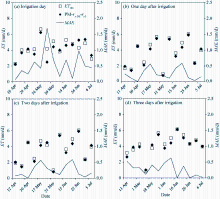
Irrigation temporally alters the water transfer in soil and crop and soil evaporation increase steadily after irrigation simply due to the readily availability of evaporative water. We then investigated the effect of irrigation on the proposed surface resistance model.

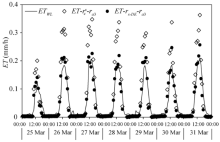
Figure 8 shows the variations of the ET estimated by the proposed surface resistance model in comparison with the measurements from the weighing lysimeter during the thirteen irrigation events (except irrigation at seedling stage) in 2016. It is evident that the results estimated from the proposed surface resistance model are in good agreement with the measurements, especially after the irrigation. In the day of the irrigation, the maximum relative error of the daily ET estimated by the proposed surface resistance model is up to 40.4%, with the MAE varying between 0.07 and 1.69 mm/d. However, one day after the irrigation the maximum relative error reduced to 11.9%, with MAE varying between 0.01 and 0.59 mm/d. Two and three days after the irrigation, the proposed surface resistance model works equally well with its maximum relative error being less than 12.5% and MAEbeing less than 0.63 mm/d.

Fig. 8

	Figure Option ViewDownloadNew Window
	Fig. 8 Comparison between the evapotranspiration estimated by the proposed surface resistance model and the measurements from the weighing lysimeter during the 13 irrigation events in 2016. MAE, mean absolute error.

The leaf stomatal resistance is an important parameter to calculate canopy resistance and depends on a number of environmental factors. Stanghellini (1987) showed that the stomatal resistance of tomatoes was affected by R_s, VPD, T_a, and CO₂ concentration. However, Jolliet and Bailey (1992) found that only the first two factors (i.e., R_s, VPD) were significant. Statistical analysis in our study showed that the stomatal resistance primarily depends on solar radiation during the daytime, and that an exponential relationship was found between the resistance and the radiation (Fig. 2). Similar results were also found for cucumber (Yang et al., 1990), waringin (Zhang and Lemeur, 1992), zucchini (Rouphael and Colla, 2004), geranium (Montero et al., 2001) and tomato (Qiu et al., 2013). The developed surface resistance model is superior to the canopy resistance model, especially when the LAIis low or during irrigation period, because the developed surface resistance model considered the combined effect of crop and soil on water vapor transfer. Soil evaporation is dominant when LAI is low and could increase steadily after irrigation. Because the canopy resistance model does not explicitly account for the water transfer in soil, using it in the PM model underestimates the ET. In contrast, the proposed model accounts for the soil surface resistance and hence improve the accuracy of the PM model. This is consistent with many other studies. For example, Stannard (1993) found that the PM model substantially underestimated the ET when the canopy resistance was significantly greater than the soil resistance. It was also found that when the canopy coverage ratio is low, using the canopy resistance in the PM model underestimated ET (Kato et al. 2004). It needs to point out that there were also studies showing that using the canopy resistance in the PM model could overestimate ET (Zhang et al., 2008; Li et al., 2014). Such controversial results are likely to be caused by changes in canopy resistance and/or soil water in root zones. For instance, with furrow irrigation or border irrigation, irrigation is less frequent and the soil resistance increases as result (approximately 800 s/m in dry soils). Consequently, the canopy resistance could reach 300 s/m in daytime as the soil dried (Zhang et al., 2008). These could combine to give rise to an overestimated ET when using the canopy resistance model.

It is worth mentioning the r_s-DE model is semi-empirical and needs calibration against experimental data. Also, its application to water-stress conditions requires verification. Therefore, the r_s-DE model needs further investigation.

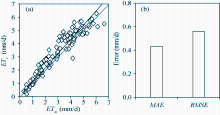
The aerodynamic resistances calculated by three models proposed by Perrier (1975a, b), Thom and Oliver (1977) and Zhang and Lemeur (1992) were compared. The r_a1 and r_a3 methods were superior and can adequately estimate the ET of tomatoes in the solar greenhouse, whereas the r_a2 method underestimated the ET. However, the applicability of the r_a1 method to greenhouse was questioned (Qiu et al., 2013) because small wind speeds within the greenhouse could result in a spurious high aerodynamic resistance. However, Mö ller et al. (2004) showed that r_a1 works well in an insect-proof greenhouse and that the water vapor transfer depended on kinetic energy of wind. Villarreal-Guerrero et al. (2012) found that the predicted ET was insensitive to the external crop resistance, and the aerodynamic resistance can be taken as a constant at 70 s/m in greenhouse. Similar findings were also reported in other studies (Kittas et al., 1999; Prenger et al., 2002). For the Stanghellini (1987) model, the average aerodynamic resistance was found to be 185 s/m for tomatoes. Ferná ndez et al. (2010, 2011) found that the FAO-56 PM model using constant aerodynamic resistance of 295 s/m accurately estimated the daily reference evapotranspiration in greenhouse. In general, the aerodynamic resistances of crops in greenhouse oscillate between 100 and 500 s/m (Bailey et al., 1993; Baille et al. 1994; Katsoulas et al. 2001). In our study, the average r_a1 was 308 s/m and was obtained from the crop and meteorological data in 2015. Figure 9 compares the daily ET estimated through replacing r_a1 by 308 s/m in the PM model with the measurement from the weighing lysimeter in 2016. The results estimated by the proposed surface resistance model were in good agreement with the measurements, with MAE and RMSEbeing 0.43 and 0.56 mm/d, respectively, slightly higher than the PM-r_s-DE-r_a3 method (MAE and RMSEbeing 0.34 and 0.45 mm/d, respectively). The convection theory is generally used to calculate the aerodynamic resistance in greenhouse where the transfer of sensible heat between canopy and the atmosphere is through convection because the wind speed is small (Zhang and Lemeur, 1992). Qiu et al. (2013) found that the PM model can accurately estimate the transpiration of hot pepper in solar greenhouse under mixed convection condition. There were also studies showing that the PM model can accurately estimate the transpirations of crops grown in different types of greenhouses when the convection is free (McAdams, 1954) or forced (Grö ber and Erk, 1961). However, these studies were conducted in temperate or maritime climate in Europe and Mediterranean, which differ from northern China in terms of environmental factors.

Fig. 9

	Figure Option ViewDownloadNew Window
	Fig. 9 Comparison between the evapotranspiration (ET) estimated by the PM-rs-DE-ra1 method (ra1=308 s/m) (ETc) and the measurements from the weighing lysimeter (ETm) in 2016 (a), as well as its errors (b). MAE, mean absolute error; RMSE, root mean square error.

As discussed above, the PM formula can estimate the ET of tomato in solar greenhouse when the LAIis low or during irrigation using the developed surface resistance model with the aerodynamic resistance calculated by mixed convection theory. A good relationship between the simulated and measured ET was found with MAE, RMSE and d_l being 0.34 mm/d, 0.45mm/d, and 0.98, respectively (Fig. 7 f and Table 2). Also, when the canopy temperature cannot be measured in greenhouse, it is acceptable to calculate the ET by setting the aerodynamic resistance as a constant of 308 s/m.