Cite this Article
YANG Jing, FANG Gonghuan, CHEN Yaning, Philippe DE-MAEYER. , Climate change in the Tianshan and northern Kunlun Mountains based on GCM simulation ensemble with Bayesian model averaging. Journal of Arid Land, 2017, 9(4): 622-634.  
Permissions
Copyright©2017, Journal of Arid Land
Received:2016-09-03 Revised:2017-06-07
Climate change in the Tianshan and northern Kunlun Mountains based on GCM simulation ensemble with Bayesian model averaging
YANG Jing1,2,*, FANG Gonghuan1,3,4, CHEN Yaning1, Philippe DE-MAEYER3,4
1 State Key Laboratory of Desert and Oasis Ecology, Xinjiang Institute of Ecology and Geography, Chinese Academy of Sciences, Urumqi 830011, China
2 National Institute of Water and Atmospheric Research, Christchurch 8011, New Zealand
3 Department of Geography, Ghent University, Ghent 9000, Belgium
4 Sino-Belgian Joint Laboratory for Geo-Information, Urumqi 830011, China
*Corresponding author: YANG Jing (E-mail: yangjing@ms.xjb.ac.cn)
Fund:National Science Foundation, Department of Energy, National Center for Atmospheric Research
Abstract

Climate change in mountainous regions has significant impacts on hydrological and ecological systems. This research studied the future temperature, precipitation and snowfall in the 21st century for the Tianshan and northern Kunlun Mountains (TKM) based on the general circulation model (GCM) simulation ensemble from the coupled model intercomparison project phase 5 (CMIP5) under the representative concentration pathway (RCP) lower emission scenario RCP4.5 and higher emission scenario RCP8.5 using the Bayesian model averaging (BMA) technique. Results show that (1) BMA significantly outperformed the simple ensemble analysis and BMA mean matches all the three observed climate variables; (2) at the end of the 21st century (2070-2099) under RCP8.5, compared to the control period (1976-2005), annual mean temperature and mean annual precipitation will rise considerably by 4.8°C and 5.2%, respectively, while mean annual snowfall will dramatically decrease by 26.5%; (3) precipitation will increase in the northern Tianshan region while decrease in the Amu Darya Basin. Snowfall will significantly decrease in the western TKM. Mean annual snowfall fraction will also decrease from 0.56 of 1976-2005 to 0.42 of 2070-2099 under RCP8.5; and (4) snowfall shows a high sensitivity to temperature in autumn and spring while a low sensitivity in winter, with the highest sensitivity values occurring at the edge areas of TKM. The projections mean that flood risk will increase and solid water storage will decrease.

Key words: climate change; GCM ensemble; Bayesian model averaging; Tianshan and northern Kunlun Mountains
1 Introduction

International Panel on Climate Change (IPCC, 2013) states that “ warming of the climate system is unequivocal” . Climate change is important to human activity as it likely changes the temporal-spatial distributions of temperature and precipitation. In the past two decades, climate change has received worldwide attention (IPCC, 2013) and the attention has been devoted to physical science basis and scenario modelling, and also to impact assessment and mitigation measures. Mountainous regions are particularly sensitive to increasing temperature and changing precipitation regimes because the variations in mountains are often larger than the global averages (Dedieu et al., 2014; Piazza et al., 2014). Therefore, climate change is likely to cause water resources and management problems in mountainous regions where snow and glaciers are important water resources to the downstream areas. For example, melt water from snow, glaciers and permafrost supplies about 80% of the total river runoff in Central Asia (Kure et al., 2013; Chen, 2014). Snowfall is sensitive to climate change in the high mountains of Asia (Kapnick et al., 2014). Therefore, it is important to understand how snowfall varies along with changing precipitation and temperature.

Previous studies showed that the Tianshan and northern Kunlun Mountains (TKM) experienced a notable climate change in the past few decades. For example, the average rising rates of air temperature and precipitation from 1940 to 1991 were about 0.1° C/10a and 12 mm/10a, respectively, in the Tianshan Mountains (Aizen et al., 1997). Li et al. (2013) also found that annual mean temperature and mean annual precipitation increased by 0.86° C and 47.3 mm, respectively, in the mountainous areas of Northwest China over the period 1960-2010. The form of precipitation (liquid or solid) is the main determining factor for river runoff (Aizen et al., 1997). Guo and Li (2015) reported that the ratio of snowfall to precipitation (snowfall fraction) experienced a downward trend in the Tianshan Mountains during 1961-2010. However, most studies mainly focused on the climate change during the past several decades and a few researches investigated the future climatic change in the 21st century for the TKM (e.g., Shi et al., 2007; IPCC, 2013). The projected temperature in the Central Asia is likely to increase by 2° C-4° C in 2081-2100 with respect to 1986-2005 under the representative concentration pathway scenarios 4.5 (RCP4.5) while precipitation is expected to decrease by 20%-30% during the wet season (from April to September) and to increase in the dry season (from October to March) by 0-40% (IPCC, 2013). Shi et al. (2007) simulated the future climate for a doubled CO2 concentration scenario based on a nested approach with the second-generation regional climate model (RegCM2), and concluded that annual mean temperature and mean annual precipitation would increase by 2° C and by 19%, respectively, for the Northwest China.

The general circulation models (GCMs) have become the main tool in future climate change assessment (IPCC, 2013). One general circulation model (GCM) projection represents only one future possibility. Combination of multiple GCM projections is expected to account for future uncertainty inherent in the GCM ensemble. Compared to the simple GCM ensemble method, the Bayesian model averaging (BMA) technique can effectively infer a probabilistic projection from several competing models and can thus produce more reliable outputs than the original ensemble (Hoeting et al., 1999; Raftery et al., 2005; Duan et al., 2007). Over the past decades, it has been widely used in weather forecasting (Sloughter et al., 2007; Fraley et al., 2010) and hydrologic modelling (Duan et al., 2007; Najafi et al., 2011; Najafi and Moradkhani, 2015). For example, the BMA gave better temperature and precipitation forecasts than those based on consensus voting of the ensemble members (Tebaldi et al., 2004; Raftery et al., 2005; Sloughter et al., 2007; Sloughter et al., 2010). Due to the pronounced advantages in producing sharp probabilistic predictions from multiple climate projections, BMA technique is increasingly used in combined climatic and hydrologic projections (Tebaldi et al., 2004; Yang et al., 2012; Liu and Xie, 2014).

This study uses a simulation ensemble of 21 GCMs from the coupled model intercomparison project phase 5 (CMIP5; IPCC, 2013) coupled with BMA to study how future precipitation (rainfall and snowfall) and temperature will change over the TKM, both spatially and temporally. The results are expected to serve the sustainable development in the TKM-related areas in Central Asia (Li et al., 2015).

2 Study area and data
2.1 Study area and observed climate data

The TKM, far away from the oceans, situates in the innermost region of the Eurasia continent. The freshwater supplies in the adjoining basins and lowlands strongly depend on the occurrence and amount of precipitation and snow/glacier melt in the region (Ososkova et al., 2000; Dietz et al., 2014). In this paper, TKM is referred to the mountainous regions of the Tianshan Mountains and north slope of the Kunlun Mountains with elevation over 1300 m a.s.l. (Fig. 1).

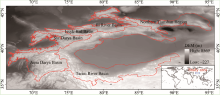Fig. 1 Topographic map of the Tianshan and northern Kunlun Mountains (TKM) with six sub-regions marked in red polygons

TKM is characterized by a continental climate with hot-dry summer and cold winter. According to the climate dataset “ Asian precipitation-highly-resolved observational data integration towards evaluation of water resources” (APHRODITE; Yasutomi et al., 2011; Yatagai et al., 2012), the annual mean temperature ranges from -9.8° C to 15.5° C and mean annual precipitation is 70-1000 mm with a large portion as snowfall. The aforementioned temperature range is basically elevation dependent and the precipitation normally increases northwestward.

In this study, the entire TKM was discretized into six sub-regions as Tarim River Basin, Northern Tianshan Region, Ili River Basin, Issyk-Kul Basin, Syr Darya Basin, and Amu Darya Basin (Fig. 1). Monthly gridded climate dataset APHRODITE was used as the observation data since it provides snowfall data in addition to precipitation and temperature. This dataset was created by interpolating station observations into 0.50° × 0.50° grid for the Asian region with a quality interpolation system (Yatagai et al., 2012). The dataset is widely used in the studies of the climate change diagnosis, water resources evaluation, and verification of model simulation and satellite precipitation estimates (www.chikyu.ac.jp/precip/scope/).

2.2 GCM simulation ensemble

Climate simulations from 1976 to 2099 were based on 21 state-of-the-art GCMs from CMIP5 for the lower emission scenario RCP4.5 and higher emission scenario RCP8.5 (Kawase et al., 2011; Van Vuuren et al., 2011). The 21 GCMs including the earth system models were from more than 20 institutes or universities (Table 1) with spatial resolutions ranging from 0.75° to 3.75° . In this study, we only considered 3 climatic variables including air temperature, precipitation and snowfall.

3 BMA technique and its application to GCM simulation ensemble
3.1 Introduction of BMA technique

BMA is a statistical way of post-processing forecast ensembles to create predictive probability density functions (PDFs) for weather and hydrological quantities (Hoeting et al., 1999). Based on BMA, for a forecast variable y with training data D=[yobs, 1, yobs, 2, ∙ ∙ ∙ , yobs, T] and K forecast models (M1, M2, …, Mk), the probability density function (PDF) of y, p(y) is given by Equation 1.

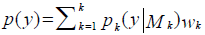
Where pk(y|Mk) the forecast PDF of y based on model Mk. wk is the likelihood of Mk being correct given the training data D, wk=p(Mk|D) with \(\sum^k_{k=1}w_k=1\). BMA predictions are the weighted averages of the individual model predictions. The conditional distribution pk(y|Mk) normally can be represented as a normal distribution, N(a0k+a1k, σ 2) gamma distribution where a0k, a1k, b0k, b1k, c0 and c1 are regression coefficients, p is the power index, σ is standard deviation and yk is the prediction of model Mk.

To apply BMA, one needs to firstly choose pk(y|Mk) (e.g., normal distribution or gamma distribution) and then determines related coefficients (i.e., a0k, a1k and σ for normal distribution, or b0k, b1k, c0, c1 and p for gamma distribution). In this study, we assumed normal distributions for temperature and power transformed gamma distributions for precipitation and snowfall as described by Sloughter et al. (2007), and coefficient estimation was based on expectation-maximization algorithm as described by Raftery et al. (2005). More details about the BMA method and expectation-maximization algorithm can refer to Raftery et al. (2005), Duan et al. (2007) and Sloughter et al. (2007).

Table 1 Information about the general circulation model (GCM) ensemble used in this study
3.2 Application procedure

First, to overcome different spatial resolutions of GCM simulations (or outputs), we firstly rescaled GCM simulation ensemble to 0.5° × 0.5° to match APHRODITE resolution with the bilinear interpolation (Aguirre-Salado et al., 2014). BMA was applied grid-wise with observation APHRODITE and GCM simulation ensemble from 1976 to 1995 to obtain a constructed statistical model on each grid, for monthly temperature, precipitation and snowfall, respectively, and then validated with monthly observation APHRODITE and GCM simulation ensemble from 1996 to 2005. Finally, these constructed grid-wise models were used to generate corresponding future climate variable predictions from 2006 to 2099.

To test our assumptions on pk(y|Mk), i.e., normal distribution for temperature and power transformed gamma distribution for precipitation and snowfall, this study adopted the approach proposed by Sloughter et al. (2010) by examining the fitted (empirical) distribution of the given observed variables, conditional on simulated values being within some bins (e.g., all observed temperatures for which the simulated temperatures were below 0° C) with the same theoretical distribution.

We used mean absolute error (MAE; Eq. 2), mean continuous ranked probability score (CRPS; Eq. 3) and the percentage of observations included in the 95% confidence interval (PI95CI) to assess the performances of the constructed BMA statistic models

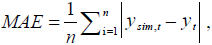
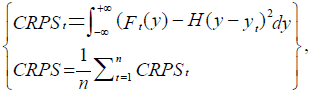
where ysim, t is the simulated value at time t by the GCM simulation ensemble or BMA technique. yt is the observation at time t; n is data length. CRPS is the mean of CRPSt at each time step t; Ft(y) is the predicted cumulative density function (CDF) at time t; H is the Heaviside function (returning zero for negative and unity for non-negative). The smaller the MAE is, the smaller the biases would be in the prediction. The smaller the CRPS is, the narrower the prediction uncertainty is. The larger PI95CI is, the better the prediction is. These indices are widely used in weather forecast as measures of the closeness of the predicted and observed cumulative distributions and sharpness of the predicted probability density function (Hersbach, 2000). As a comparison, these three indices were also calculated for GCM simulation ensemble.

4 Results

The general performances of BMA technique were firstly demonstrated for three climate variables with observations and compared to GCM simulation ensemble for the periods 1976-1995 (to construct the BMA model) and 1996-2005 (to validate the BMA performance). BMA technique was then performed to obtain future climate predictions for the period 2006-2099 under both RCP4.5 and RCP8.5 scenarios. Since changes for each climate variable had a monotonic trend in three periods of 2010-2039, 2040-2069, and 2070-2099, we only compared the differences between the prediction period of 2070-2099 (the last 30 years in the end of the 21st century) and the control period of 1976-2005 (the first 30 years of 1975-2099).

4.1 Performance of BMA technique

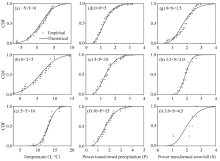
CDF of observed climate variables conditional on the GCM simulation bins can be fitted reasonably well using a normal distribution for temperature and a power transformed gamma distribution for precipitation and snowfall as Figure 2 except for Figure 2i due to insufficient observed snowfall data. Similar results can be obtained for other GCM simulations and grids. All these demonstrate that our assumptions on pk(y|Mk) are reasonable.

For all the three climate variables, BMA technique outperformed GCM simulation ensemble for both training period and validation period with substantially reduced MAE and CRPS values and greatly increased PI95CI (Table 2). For the validation period 1996-2005, for temperature, MAE and CRPS were reduced from 7.5° C and 8.2° C to 1.4° C and 1.0° C, respectively, and PI95CI increased from 45% to 93%; for precipitation, MAE and CRPS were reduced from 24.4 to 10.2 mm and 31.1 to 7.3, respectively, and PI95CI increased from 60% to 91%. For snowfall, MAE and CRPS were reduced from 12.6 to 4.4 mm and 15.9 to 3.2, respectively, and PI95CI increased considerably from 63% to 94%.

For annual mean temperature variations over space, observation was generally high in low-elevation areas and low in high-elevation areas. The spatially averaged mean was 2.8° C with a range of -9.0° C-16.3° C in TKM (Fig. 3). Compared to observation (Fig. 3a1), the mean of GCM simulation ensemble (Fig. 3b1) had an obvious over-estimate in high-elevation areas in northern TKM and an extreme over-estimate in western TKM. Nevertheless, the BMA mean of GCM simulation ensemble (Fig. 3c1) had a good spatial match with the observation with the majority of biases concentrated in 0° C-1° C (Fig. 4a).

For mean annual precipitation, observation was high in the west and low in the east and south. The spatially averaged mean was 237 mm with a range of 33.4-833 mm (Fig. 3a2). Obviously, the ensemble mean over-estimated the precipitation in the south part (Fig. 3b2), while BMA means matched with the observation quite well spatially (Fig. 3c2) with the majority of biases concentrated in 0-100 mm (Fig. 4b).

Fig. 2 Examples of the fitted (empirical) cumulative density function (CDF) plots for observed climate variables conditional on one general circulation model (GCM) forecasts being within some bins: normal distribution for temperature (a, b and c) and power transformed gamma distribution for observed precipitation (d, e and f) and snowfall (g, h and i)

For mean annual snowfall, its spatial pattern of observation is similar to precipitation (Fig. 3a3). The GCM ensemble mean has an under-estimate in the west TKM and an overestimate in the south TKM (Fig. 3b3). The BMA mean (Fig. 3c3) gives a fairy good spatial match with the observation and its spatial biases concentrate in 0-40 mm (Fig. 4c) given the average observation being 93.0 mm with a range of 2.4-461.3 mm. Compared to observation, snowfall biases are small. The large estimation errors occur only on several grids in the north and west (Figs. 4d-f). Compared to GCM simulation ensemble, BMA has improved estimates in all these three variables and BMA means match relatively well with the observations (Fig. 3).

Table 2 Performances of the Bayesian model averaging (BMA) technique and the general circulation model (GCM) ensemble for temperature, precipitation and snowfall simulations for 1976-1995 (training period) and 1996-2005 (validation period)

Fig. 3 Observation (a1, a2 and a3), mean of GCM simulation ensemble (b1, b2 and b3) and the Bayesian model averaging (BMA) mean of GCM simulation ensemble (c1, c2 and c3) for mean annual temperature, precipitation and snowfall during 1996-2005

Fig. 4 Spatial biases between observation and BMA mean of GCM simulation ensemble with histograms during 1996-2005

4.2 Future climate changes

At the end of the 21st century, the spatial patterns of temperature, precipitation and snowfall are close to those in the control period (Figs. 5a1-3). For temperature, high values are distributed in low-elevation areas while low values in high-elevation areas. For precipitation and snowfall, values remain high in the west and low in the east and south with a less spatial heterogeneity for snowfall.

Generally, there is an increase in temperature for the entire region and the mean temperature will increase by 4.8° C for 2070-2099 (the end of the 21st century) with spatial increases ranging from 3.3° C to 7.1° C (Fig. 5b1). The average annual change rate (Fig. 5c1) is 0.052° C/a ranging from 0.036° C/a to 0.069° C/a. Spatially, the increase rate is the highest in the southwest (most part of the Amu Darya Basin). Nearly all models give annual changing rates larger than the global average.

Fig. 5 Spatial distribution of the annual mean temperature (a), mean annual precipitation (b) and mean annual snowfall (c) during 2070-2099 (a1-3), the absolute changes compared to 1976-2005 (b1-3), annual change rates from 1976 to 2099 (c1-3) and GCM consistencies (d1-3) based on higher emission scenario RCP8.5. GCM consistency is defined as the percentage of GCMs with change rate greater than 0.037° C/a (i.e. global warming rate under RCP8.5) for temperature and positive change rates for precipitation and negative change rates for snowfall.

Mean annual precipitation will increase from 187.5 mm in the control period to 197.3 mm for 2070-2099 with relative increase being 5.2% and the increment is higher in the north than in the south and west (Fig. 5b2). Annual precipitation change rate (Fig. 5c2) will be 0.10 mm/a with a slight increase in the central Tianshan Mountains (about 0.4 mm/a) and a slight decrease in the northern Kunlun Mountains (about 0.2 mm/a). Clearly, over 70% of the GCM models give an increased precipitation in the east while only 40% of the GCMs for the western TKM (Fig. 5d2).

Mean annual snowfall will generally experience a decrease from 76.2 mm in the control period to 56.0 mm in 2070-2099 (relative decrease is 26.5%) with average changes ranging from -120 mm in the west to 40 mm in the high mountains in the east (Fig. 5b3). The annual change rate during 1976-2099 is -0.22 mm/a. Substantial decrease is expected in the western TKM. Most models demonstrate a decreasing trend (GCM consistency is approaching 100%) in most areas except the northeastern part. Seasonally, snowfall shows considerable decrease in the western region in autumn, winter and spring (Fig. 6). Slight increase is only projected on several grids in the central Tianshan Mountains in winter. Similar results were obtained for RCP4.5 except that the magnitude is smaller than that for RCP8.5.

Fig. 6 Changes of mean seasonal snowfall during 2070-2099 compared to 1976-2005 under RCP8.5

On the basin scale, all basins will experience increases in temperature and precipitation (except the Amu Darya Basin) and decreases in snowfall (Fig. 7). Temperature change will be around 2.4° C-3.0° C for RCP4.5 and 4.2° C-5.3° C for RCP8.5 with larger increments in the Tarim River Basin (3.0° C and 5.3° C), the Ili River Basin (2.7° C and 4.7° C) and the Amu Darya Basin (2.6° C and 4.6° C). Precipitation shows an overall increasing trend (except in the Amu Darya Basin) with changing magnitude being -0.8%-10.6% under RCP4.5 and being -1.8%-12.9% under RCP8.5. Compared to precipitation, snowfall shows obvious decreasing trend. Decrease in snowfall is the largest in the Amu Darya Basin (-22.16% and -38.22%), followed in a decreasing order by the Syr Darya Basin (-15.60% and -30.36%), the Issyk-Kul Basin (-13.84% and -25.18%), the Tarim River Basin (-10.50% and -20.79%), the Ili River Basin (-7.29% and -15.27%) and northern Tianshan region (-4.69% and -10.03%) under RCP4.5 and RCP8.5, respectively.

Fig. 7 Future climatic changes during 2070-2099 compared to 1976-2005 under the representative concentration pathway (RCP) lower emission scenario RCP4.5 and higher emission scenario RCP8.5 for the TKM and its six sub-regions. T, temperature; P, precipitation; S, snowfall; Snowfall fraction, ratio of snowfall to precipitation.

4.3 Snowfall fraction

Snowfall fraction (ratio of snowfall to precipitation) was used to study the shift of snowfall to rainfall. Compared to the control period, snowfall fraction in most areas will decrease essentially in 2070-2099 under both RCP4.5 and RCP8.5 (Fig. 7), except that in winter for the Amu Darya Basin under RCP4.5. Average snowfall fraction ratios decrease from 0.63 (0.53-0.69 for the sub-regions) in the control period to 0.52 (0.46-0.58) under RCP4.5 and 0.45 (0.41-0.50) under RCP8.5.

Seasonally, snowfall fraction decreases dramatically in the transient seasons (October, November, March, April) and only slightly in the coldest season (January and February) in the Northern Tianshan Region, the Ili River Basin and the Amu Darya Basin. In the western regions of the Issyk-Kul Basin and the Syr Darya Basin, snowfall fraction decreases almost evenly among the twelve months while snowfall fraction decreases most significantly in the coldest months in the Tarim Basin.

As shown in Figure 8, the annual map of sensitivity of snowfall to temperature shows that in most areas temperature will have a negative impact on snowfall (97% of grids) and the most sensitive area is in the west. Sensitivity values range from -32.6%/° C to 4.3%/° C with 90% quantile between -16.2%/° C and 0.9%/° C. Seasonally, the negative impact is significant in most areas of TKM during autumn and spring, while in winter the positive impact is significant in high mountains. The 90% quantile of sensitivity values mainly ranges from -31.9%/° C to -1.1%/° C in autumn and from -29.3%/° C to -1.2%/° C in spring. In winter, the responses of snowfall to temperature are hardly to observe for the most areas of TKM with sensitivity values ranging from -13.2%/° C to 4.4%/° C. The eastern Tianshan Mountains is an exception where both temperature and snowfall will increase. Annual sensitivity of snowfall to precipitation is only significant in west and southwest parts.

Fig. 8 Sensitivity distribution of relative snowfall change (δ S) to absolute annual temperature change (∆ T) and to relative precipitation change (δ P) for annual (a, e), autumn (b, f), winter (c, g) and spring (d, h).

5 Discussion

We applied the BMA technique to statistically post-processing the output ensemble of 21 GCMs for producing more informative and sharper probabilistic distributions of the targeted climate variables. From above listed results (Fig. 2), the assumptions of normal distribution for temperature and power transformed gamma distribution for precipitation and snowfall seem rather reasonable. It should be added that these distributions were successfully applied in the North American Pacific Northwest, the Netherlands and the Huaihe River Basin of China (Sloughter et al., 2007; Schmeits and Kok, 2010; Liu and Xie, 2014). The BMA processed simulation outperformed the GCM output ensemble with a narrower prediction uncertainty than the original ensemble in terms of CRPS and MAE. The application of BMA technique in the TKM shed a light on future precipitation and snowfall predictions.

Snowfall is expected to continue its decreasing trend despite a slight increase in precipitation. The decreased snowfall fraction has been detected in the Karakoram and Tianshan Mountains, the contiguous United States and the Alps during the past few decades (Feng and Hu, 2007; Serquet et al., 2011; Berghuijs et al., 2014; Guo and Li, 2015) and is expected to decrease across much of the Northern Hemisphere in the 21st century (Winkelmann et al., 2012; O’ Gorman, 2014). Intuitively speaking, it is highly likely that the snowfall fraction will decrease with increasing temperature.

The decreased snowfall and snowfall fraction are mainly result from the projected rising temperature and are further aggravated by the projected decreasing precipitation in the Amu Darya Basin. The 90% quantile values of sensitivity of snowfall to temperature range from -16.2%/° C to -0.9%/° C. It means that with a 1° C temperature increase, snowfall will decrease by 16.2% to 0.9%. The response of snowfall to temperature varies with seasons and elevations. As concluded by Mir et al. (2015), “ snowfall trends are more sensitive to climate change below an elevation of 4000 m a.s.l.” . For the high mountains in the eastern Tianshan Mountains, temperature has a positive impact on snowfall with sensitivity being about 5%/° C, which is consistent with the studies in the high Alps of 10%/° C (Hezel et al., 2012) and the cold Antarctic of 5%/° C (Monaghan et al., 2008). The negative impact could happen “ as warmer conditions would increase the amount of precipitation that falls as rain relative to snow” (Davis et al., 1999), while the positive impact could happen “ since saturation vapor pressure increases exponentially as a function of temperature, thereby allowing for the possibility of a more moist atmosphere” (Davis et al., 1999) as far as temperature is still lower than snowfall point. In non-winter seasons (summer, autumn and spring), temperature increase will most likely decrease the snowfall. In winter, as temperature in the high mountains is normally below 0° C, precipitation increase simply means snowfall increase.

The shift from snowfall to rainfall could be quite important in TKM because such changes could influence the timing of spring runoff, causing water shortage in summer and sometimes resulting in floods (Feng and Hu, 2007; Bocchiola, 2014). Accompanying the decreasing snowfall fraction, the glacier extent is expected to decrease under a warmer climate. It will reduce the current glacier extent by 36%-45% when the temperature rise 2.2° C-3.1° C (Hagg et al., 2013). A strong warming could pose a great risk on glacier- and snow-storage of water and therefore decrease long-term water availability (Chen et al., 2016).

6 Conclusions

This paper evaluated air temperature, precipitation and snowfall changes in the TKM using BMA technique based on a simulation ensemble of 21 GCMs from CMIP5. We concluded that, BMA technique significantly outperformed GCM simulation ensemble and can thus be used for future climate change assessment. Second, the TKM will experience a dramatic increase in mean temperature at an annual rate of 0.052° C/a, a slight increase in mean annual precipitation at a rate of 0.10 mm/a and a significant decrease in snowfall at a rate of 0.22 mm/a under RCP8.5 during 1976-2099. Third, temperature will increase in all basins that are hydrologically associated with TKM. Precipitation will increase in nearly all basins with an exception of the Amu Darya and snowfall will decrease in the following basins (in a decreasing order of the projected decreasing magnitude): Amu Darya Basin, Syr Darya Basin, Issyk-Kul Basin, Tarim Basin, Ili Basin and Northern Tianshan Region; Fourth, snowfall fraction decreases substantially from 0.63 in the control period (1976-2005) to 0.41 for the end of 21st century (2070-2099) under RCP8.5. Snowfall shows a high sensitivity to temperature in autumn and spring (the 90% quantile ranging from -31.9%/° C to -1.1%/° C and from -29.3%/° C to -1.2%/° C) and a low sensitivity in winter (from -13.2%/° C to 4.4 %/° C). It should be particularly noted that temperature rising is projected to increase snowfall only in the high mountains in winter.

Acknowledgements

The research was supported by the Thousand Youth Talents Plan (Xinjiang Project), the National Natural Science Foundation of China (41630859) and the West Light Foundation of Chinese Academy of Sciences (2016QNXZB12). We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modeling groups (listed in Table 1 of this paper) for their efforts in producing their model outputs. For CMIP the U.S. Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals.

The authors have declared that no competing interests exist.

Reference
1 Aguirre-Salado C A, Treviño-Garza E J, Aguirre-Calderón O A, et al. 2014. Mapping aboveground biomass by integrating geospatial and forest inventory data through a k-nearest neighbor strategy in North Central Mexico. Journal of Arid Land , 6(1): 80-96. [Cited Within:1]
2 Aizen V B, Aizen E M, Melack J M, et al. 1997. Climatic and hydrologic changes in the Tien Shan, central Asia. Journal of Climate, 10(6): 1393-1404. [Cited Within:2]
3 Berghuijs W R, Woods R A, Hrachowitz M. 2014. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nature Climate Change, 4(7): 583-586. [Cited Within:1]
4 Bocchiola D. 2014. Long term (1921-2011) hydrological regime of Alpine catchments in Northern Italy. Advances in Water Resources, 70: 51-64. [Cited Within:1]
5 Chen Y N. 2014. Water Resources Research in Northwest China. Dordrecht, Netherland s: Springer, 1-440. [Cited Within:1]
6 Chen Y N, Li W H, Deng H J, et al. 2016. Changes in central Asia’s water tower: past, present and future. Scientific Reports, 6: 35458, doi: DOI:10.1038/srep35458. [Cited Within:1]
7 Davis R E, Lowit M B, Knappenberger P C, et al. 1999. A climatology of snowfall-temperature relationships in Canada. Journal of Geophysical Research: Atmospheres, 104(D10): 11985-11994. [Cited Within:2]
8 Dedieu J P, Lessard-Fontaine A, Ravazzani G, et al. 2014. Shifting mountain snow patterns in a changing climate from remote sensing retrieval. Science of the Total Environment, 493: 1267-1279. [Cited Within:1]
9 Dietz A, Conrad C, Kuenzer C, et al. 2014. Identifying changing snow cover characteristics in central Asia between 1986 and 2014 from remote sensing data. Remote Sensing, 6(12): 12752-12775. [Cited Within:1]
10 Duan Q Y, Ajami N K, Gao X G, et al. 2007. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Advances in Water Resources, 30(5): 1371-1386. [Cited Within:3]
11 Feng S, Hu Q. 2007. Changes in winter snowfall/precipitation ratio in the contiguous United States. Journal of Geophysical Research: Atmospheres, 112(D15): D15109. [Cited Within:2]
12 Fraley C, Raftery A E, Gneiting T. 2010. Calibrating multimodel forecast ensembles with exchangeable and missing members using Bayesian model averaging. Monthly Weather Review, 138(1): 190-202. [Cited Within:1]
13 Guo L P, Li L H. 2015. Variation of the proportion of precipitation occurring as snow in the Tian Shan Mountains, China. International Journal of Climatology, 35(7): 1379-1393. [Cited Within:1]
14 Hagg W, Hoelzle M, Wagner S, et al. 2013. Glacier and runoff changes in the Rukhk catchment, upper Amu-Darya basin until 2050. Global and Planetary Change, 110: 62-73. [Cited Within:1]
15 Hersbach H. 2000. Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather and Forecasting, 15(5): 559-570. [Cited Within:1]
16 Hezel P J, Zhang X, Bitz C M, et al. 2012. Projected decline in spring snow depth on Arctic sea ice caused by progressively later autumn open ocean freeze-up this century. Geophysical Research Letters, 39(17): L17505. [Cited Within:1]
17 Hoeting J A, Madigan D, Raftery A E, et al. 1999. Bayesian model averaging: a tutorial. Statistical Science, 14(4): 382-401. [Cited Within:2]
18 IPCC. 2013. Climate Change 2013: the Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom, New York, NY, USA: Cambridge University Press. [Cited Within:6]
19 Kapnick S B, Delworth T L, Ashfaq M, et al. 2014. Snowfall less sensitive to warming in Karakoram than in Himalayas due to a unique seasonal cycle. Nature Geoscience, 7(11): 834-840. [Cited Within:1]
20 Kawase H, Nagashima T, Sudo K, et al. 2011. Future changes in tropospheric ozone under Representative Concentration Pathways (RCPs). Geophysical Research Letters, 38(5): L05801. [Cited Within:1]
21 Kure S, Jang S, Ohara N, et al. 2013. Hydrologic impact of regional climate change for the snow-fed and glacier-fed river basins in the Republic of Tajikistan: statistical downscaling of global climate model projections. Hydrological Processes, 27(26): 4071-4090. [Cited Within:1]
22 Li B F, Chen Y N, Chen Z S, et al. 2013. Variations of temperature and precipitation of snowmelt period and its effect on runoff in the mountainous areas of Northwest China. Journal of Geographical Sciences, 23(1): 17-30. [Cited Within:1]
23 Li P Y, Qian H, Howard K W F, et al. 2015. Building a new and sustainable “Silk Road economic belt”. Environmental Earth Sciences, 74(10): 7267-7270. [Cited Within:1]
24 Liu J G, Xie Z H. 2014. BMA probabilistic quantitative precipitation forecasting over the Huaihe basin using TIGGE multimodel ensemble forecasts. Monthly Weather Review, 142(4): 1542-1555. [Cited Within:2]
25 Mir R A, Jain S K, Saraf A K, et al. 2015. Decline in snowfall in response to temperature in Satluj basin, western Himalaya. Journal of Earth System Science, 124(2): 365-382. [Cited Within:1]
26 Monaghan A J, Bromwich D H, Schneider D P. 2008. Twentieth century Antarctic air temperature and snowfall simulations by IPCC climate models. Geophysical Research Letters, 35(7): L07502. [Cited Within:1]
27 Najafi M R, Moradkhani H. 2015. Multi-model ensemble analysis of runoff extremes for climate change impact assessments. Journal of Hydrology, 525(0): 352-361. [Cited Within:1]
28 Najafi M R, Moradkhani H, Jung I W. 2011. Assessing the uncertainties of hydrologic model selection in climate change impact studies. Hydrological Processes, 25(18): 2814-2826. [Cited Within:1]
29 O'Gorman P A. 2014. Contrasting responses of mean and extreme snowfall to climate change. Nature, 512(7515): 416-418. [Cited Within:1]
30 Ososkova T, Gorelkin N, Chub V. 2000. Water resources of central Asia and adaptation measures for climate change. Environmental Monitoring and Assessment, 61(1): 161-166. [Cited Within:1]
31 Piazza M, Boé J, Terray L, et al. 2014. Projected 21st century snowfall changes over the French Alps and related uncertainties. Climatic Change, 122(4): 583-594. [Cited Within:1]
32 Raftery A E, Gneiting T, Balabdaoui F, et al. 2005. Using Bayesian model averaging to calibrate forecast ensembles. Monthly Weather Review, 133(5): 1155-1174. [Cited Within:4]
33 Schmeits M J, Kok K J. 2010. A comparison between raw ensemble output, (Modified) Bayesian model averaging, and extended logistic regression using ECMWF ensemble precipitation reforecasts. Monthly Weather Review, 138(11): 4199-4211. [Cited Within:1]
34 Serquet G, Marty C, Dulex J P, et al. 2011. Seasonal trends and temperature dependence of the snowfall/precipitation-day ratio in Switzerland . Geophysical Research Letters, 38(7): L07703. [Cited Within:1]
35 Shi Y F, Shen Y P, Kang E S, et al. 2007. Recent and future climate change in northwest China. Climatic Change, 80(3): 379-393. [Cited Within:1]
36 Sloughter J M, Raftery A E, Gneiting T, et al. 2007. Probabilistic quantitative precipitation forecasting using Bayesian model averaging. Monthly Weather Review, 135(9): 3209-3220. [Cited Within:5]
37 Sloughter J M, Gneiting T, Raftery A E, 2010. Probabilistic wind speed forecasting using ensembles and Bayesian model averaging. Journal of the American Statistical Association, 105(489): 25-35. [Cited Within:2]
38 Tebaldi C, Mearns L O, Nychka D, et al. 2004. Regional probabilities of precipitation change: A Bayesian analysis of multimodel simulations. Geophysical Research Letters, 31(24): L24213, doi: DOI:10.1029/2004GL021276. [Cited Within:2]
39 van Vuuren D P, Edmonds J, Kainuma M, et al. 2011. The representative concentration pathways: an overview. Climatic Change, 109(1-2): 5-31. [Cited Within:1]
40 Winkelmann R, Levermann A, Martin M A, et al. 2012. Increased future ice discharge from Antarctica owing to higher snowfall. Nature, 492(7428): 239-242. [Cited Within:1]
41 Yang T, Hao X B, Shao Q X, et al. 2012. Multi-model ensemble projections in temperature and precipitation extremes of the Tibetan Plateau in the 21st century. Global and Planetary Change, 80-81: 1-13. [Cited Within:1]
42 Yasutomi N, Hamada A, Yatagai A. 2011. Development of a long-term daily gridded temperature dataset and its application to rain/snow discrimination of daily precipitation. Global Environmental Research, 15: 165-172. [Cited Within:1]
43 Yatagai A, Kamiguchi K, Arakawa O, et al. 2012. APHRODITE: constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bulletin of the American Meteorological Society, 93(9): 1401-1415. [Cited Within:2]