The experiment was conducted in 2012 at Shiyanghe Experimental Station for Water-Saving in Agriculture and Ecology, China Agricultural University, in Wuwei City, Gansu Province of Northwest China (37° 52′ N, 102° 51′ E; 1581 m a.s.l.). The region is characterized by a continental arid climate, with annual average temperature of 8.8° C, average annual precipitation of 164.4 mm and average annual pan evaporation of 2000 mm. Solar radiation is abundant with average sunshine of 3000 h/a. The average frost-free period is 150 d/a. Groundwater table in this region is below 25-m deep.

The solar greenhouse used in this study was constructed from a steel frame in 2007, covered with a thermal polyethylene sheet. A roof ventilation system was used to control the interior microclimate. More detailed description of the solar greenhouse can be found in Qiu et al. (2011). The soil in the solar greenhouse is silt loam with average bulk density of 1.46 g/cm³, average field water capacity of 0.36 cm³/cm³ and average wilting point of 0.13 cm³/cm³. Soil texture at depths of 0-100 cm is composed of 12.6% clay, 64.3% silt and 23.1% sand. Irrigation water is from a nearby well with electrical conductivity of 0.52 dS/m.

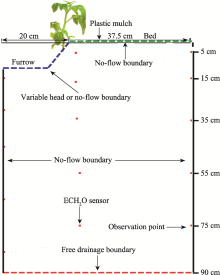
A common local variety of tomato (Solanum lycopersicum L., cultivar Oyadi) was used in the experiment. The tomato plants were transplanted on 28 February, 2012. Two rows of seedlings with one seedling per hole were evenly transplanted along the edge of each furrow row (40 cm between rows and 40 cm between plants within a row). The widths of the bed and nearby furrow were 75 and 40 cm, respectively (Fig. 1). A more detailed description of the planting pattern can be found in Qiu et al. (2013). Tomato plants were cultivated in a north-south direction. We covered the soil with clear polyethylene film (1.2 m wide and 5 μ m thick) along each row (furrow plus bed) after transplanting to reduce soil evaporation and to increase soil temperature. We irrigated the tomato plants with 27.9 mm water during transplanting and also on 12^th day after transplanting (DAT) to keep the seedlings alive and to enhance growth of transplanted plants. From 12 DAT, plants were irrigated to 90% of field water capacity (θ _F) when the mean soil volumetric water content (θ _i) in the main root zone (Z_r=0.5 m) was depleted to 75% (± 2%) of θ _F. For each irrigation event, the amount of water irrigated (D; mm) was calculated as follows:

D=1000× (0.9θ _F-θ _i)× Z_r. (1)

Irrigation water was applied to the blocked-end furrow, and the amount of water irrigated for each irrigation event was measured by a water meter.

Fig. 1

	Figure Option ViewDownloadNew Window
	Fig. 1 Schematic diagram of planting pattern and soil core sampling

ECH₂O sensors (Decagon Devices, Pullman, WA, USA) were used to observe soil water content with an accuracy of ± 3% and the data were recorded every 30 min using EM 50 data loggers (Decagon Devices, Pullman, WA, USA). Three sets of ECH₂O sensors were placed (5 sensors per set), i.e., one set in the center of the furrow, one set at the edge of the furrow, and one set in the center of the bed. The 5 sensors in each set were placed at depths of 0-10, 10-20, 20-40, 40-60 and 60-80 cm, respectively.

We measured the sap flow of tomato plants by the heat balance method with the Flow 32-1K system (Model SGA 13-WS, Dynamax, Houston, TX, USA). Sap flow of two tomato plants was monitored from 4 June to 19 June and from 21 June to 4 July, 2012. The two tomato plants were randomly selected with plant diameters ranging from 12 to 16 mm. Two sensors of the Flow 32-1K system were installed at a height of 10-20 cm above the ground surface. According to the standard procedure, in normal (default) mode, the lower flow filter is activated when the heat conveyed by the sap is ≤ 20% of the power input to the stem from the heater and when the change in temperature is ≤ 0.75° C. The higher flow filter is activated at a maximum normalized sap velocity of 152 cm/h. Sap flow data were collected at an interval of 5 s and the 15-min average values were recorded by a CR 1000 data logger (Campbell Scientific, Logam, UT, USA). The average of two readings was used as the input for the time-variable boundary condition in the HYDRUS-2D model.

Root density length distribution varies with both soil depth and radial distance from the plant. Soil core samples were taken using a root auger with 6-cm diameter around each of three selected tomato plants at the end of the experiment. Soil core samples were taken in four different directions around each tomato plant at soil depths of 0-80 cm with an interval of 10 cm (Fig. 1), and in total, 120 soil cores were taken for each plant. It should be noted that fewer roots were distributed at the 80-100 cm depth (Machado et al., 2003). The radial distance from the plant was 39 cm in the east direction (the bed side, almost half of the width of a bed) and 21 cm (almost half of the distance within a row) in each of the other three directions (i.e., west, north, and south). Soil core samples were washed with fresh water to isolate the roots. Then, root length of the fine roots (diameter< 2 mm; the main roots for water uptake) was measured using a scanner (Regent Instruments Inc., Canada). Root length density of each soil core sample was calculated as the ratio of the total root length in each soil core sample to each core volume.

The HYDRUS-2D model uses numerical methods to solve the Richards’ equation for saturated-unsaturated water flow (Š imů nek et al., 2006):

$\frac{\partial \theta (h)}{\partial t}=\frac{\partial }{\partial r}[K(h)\frac{\partial h}{\partial r}]+\frac{\partial }{\partial z}[K(h)\frac{\partial h}{\partial z}]-\frac{\partial K(h)}{\partial z}-S(r, z, t), $ (2)

where θ is the soil water content (cm³/cm³); h is the pressure head (cm); K(h) is the unsaturated hydraulic conductivity (cm/min); z is the vertical coordinate (cm), where upward is assumed to be positive; r is the horizontal coordinate (cm), which is positive for the bed side (east direction) and negative for the furrow side (west direction); t is the time (day); and S is a sink term accounting for root water uptake (unit of per day). The sink term can be calculated as the distribution of the potential transpiration rate (cm/d) over the root zone using the normalized root length density distribution function (b(r, z, t); unit of per cm) multiplied by the dimensionless water stress response function (γ (h)) (Feddes et al., 1978; Š imů nek and Hopmans, 2009; Gonzá lez et al., 2015):

$S(r, z, t)=\gamma (h){{S}_{p}}(r, z, t)=\gamma (h)b(r, z, t){{L}_{t}}{{T}_{p}}, $ (3)

where S_p(r, z, t) is the volume of water removed from a unit volume of soil per unit of time (cm³/(cm³• d)), and L_t is the surface root length associated with transpiration (cm). In Equation 3, γ (h) includes the following parameters: P₀ is the pressure head value that roots start to extract water from the soil; P_Opt is the pressure head value that roots extract water at the maximum possible rate; P_2H and P_2L are the limiting pressure head values, below which roots no longer extract water at the maximum possible rate (assuming potential transpiration rates ofr_2H and r_2L, respectively); and P₃ is the pressure head value that root water uptake stops (usually equal to the wilting point). The following parameter values from the HYDRUS-2D database (Š imů nek et al., 2006) were used in this study: P₀= -10 cm, P_Opt= -25 cm, P_2H= -800 cm, P_2L= -1500 cm, P₃= -8000 cm, r_2H=0.01 cm/d, and r_2L=0.1 cm/d.

2.3.1 Soil hydraulic properties

The following equations were used to obtain the parameters of soil water retention curve and unsaturated hydraulic conductivity (Van Genuchten, 1980):

$\theta ={{\theta }_{r}}+({{\theta }_{s}}-{{\theta }_{r}}){{[1+{{(\alpha S)}^{n}}]}^{-m}}\text{ (}m=1-1/n\text{), }$ (4)

$K(\theta )={{K}_{s}}S_{e}^{l}[1-{{(1-S_{e}^{l/m}]}^{2}}, $ (5)

$S{}_{e}=\frac{\theta -{{\theta }_{r}}}{{{\theta }_{s}}-{{\theta }_{r}}}, $ (6)

where θ is the soil water content (cm³/cm³); θ _s is the saturated soil water content (cm³/cm³); θ _r is the residual soil water content (cm³/cm³); n, m, α and l are empirical shape parameters (dimensionless); K(θ ) is the unsaturated hydraulic conductivity function; K_s is the saturated hydraulic conductivity; and S_e is the effective water content (dimensionless).

The computer program Retention Curve Program for Unsaturated Soils (Van Genuchten et al., 1998), estimations from the Rosetta neural network model (Schaap, 1999), and observed soil physical properties were used to determine soil hydraulic parameters in the solar greenhouse. Soil hydraulic parameter values used in HYDRUS-2D model are listed in Table 1.

Table 1

Table 1

Table 1 Soil hydraulic parameters used in HYDRUS-2D model θ r (cm3/cm3) θ s (cm3/cm3) α Ks (cm/d) n m l 0.10 0.392 0.023 12.87 1.22 0.18 0.5

Table 1 Soil hydraulic parameters used in HYDRUS-2D model

2.3.2 Flow domain, initial and boundary conditions

Water flow in the root zone in this study was represented by a two-dimensional flow domain with 57.5-cm width (representing half of a 40-cm wide furrow and half of a 75-cm wide bed at the upper boundary) and 90-cm depth (Fig. 2). The flow domain was discretized into 2129 fi nite nodes and 4469 triangular elements. Fifteen observation points were set in the HYDRUS-2D model, with 5 located in the center of the furrow, 5 at the edge of the furrow, and 5 at the center of the bed (Fig. 2). The 5 observation points were set at soil depths of 5, 15, 35, 55, and 75 cm, respectively.

Fig. 2

	Figure Option ViewDownloadNew Window
	Fig. 2 Schematic of the flow domain and boundary conditions of the flow domain

Soil water contents observed before the simulation started were used as the initial conditions for the flow domain. Boundary conditions of the flow domain that were used to simulate the water flow from the furrow irrigation are shown in Figure 2. By symmetry, no-flow boundary condition was used at the left and right sides of the flow domain. As ground water table in the study area is below 25 m, the effect of groundwater was not considered, and the free drainage boundary condition was used at the bottom of the flow domain (z= -90 cm). It should be particularly noted that we ignored evaporation from the soil surface because the plastic mulch prevents most of the evaporation and only less than 5.6% of evapotranspiration is from soil evaporation when plastic film is used (Qiu et al., 2015). Thus, the furrow and bed surfaces were set as no-flow boundary conditions when no irrigation events occurred. During irrigation, both sides of the furrow were changed to variable flux boundary conditions.

When the initial soil water content (before irrigation) was at a critical level such that tomato plants started to suffer water stress, we irrigated tomato plants with an amount (I) at a given potential transpiration rate (T_p) over a period of time (one irrigation cycle). Soil water content (θ ), potential transpiration rate (T_p), and deep percolation amount (D) in this period (one irrigation cycle) can be simulated by the HYDRUS-2D model. The relationship between irrigation interval (Q), I and D in this period (one irrigation cycle) can be obtained according to the critical level of soil water content (i.e., when tomato plant started to suffer water stress). The same relationship can be used in the next irrigation cycle if the T_p is the same.

In this study, the Q-I-D relationship was analyzed for a low T_p (a daily average of 1.5 mm/d, usually during winter and spring), a medium T_p (a daily average of 2.7 mm/d) and a high T_p (a daily average of 4 mm/d, usually during summer). There are costs for both irrigation water and irrigation operation. We can adopt a high irrigation frequency with a low amount of water used for each irrigation event when the restriction of water use is the priority. By contrast, when it is important to minimize the cost of irrigation operation, infrequent irrigation with a large amount of water for each irrigation event can be used. However, there may be drainage water for the latter case. Suitable irrigation intervals and irrigation amounts can be obtained according to the Q-I-D relationship determined under different T_p values.

SPSS version 21.0 (IBM Corp., Armonk, NY, USA) was used for linear and non-linear regression analyses of root length density distribution. Surfer software (Golden Software, Inc., Golden, USA) was used to graphically display the observed two-dimensional root length density distribution and soil water content. HYDRUS-2D model provided the simulated two-dimensional root length density graphically. Simulation of soil water dynamics was run from 4 June to 19 June and from 21 June to 4 July, 2012 (30 days) at the fruit bearing and harvesting stages, respectively. It should be pointed out that root length density distribution was relatively stable at these two stages.

Linear correlation with a zero intercept (i.e., y=bx) between simulated and observed soil water content values was used to assess the accuracy of the model simulations. Model performance was also evaluated using the coefficient of determination (R²), mean absolute error (MAE), root mean square error (RMSE), mean relative error (MRE), and index of agreement (d_IA) (Willmott, 1981; Willmott and Matsuura, 2005; Martins et al., 2013).

$MAE=\frac{1}{N}\sum\limits_{i=1}^{N}{\left| {{O}_{i}}-\left. {{S}_{i}} \right| \right.}, $ (7)

$RMSE={{\left[ \frac{\sum\nolimits_{i=1}^{N}{{{({{O}_{i}}-{{S}_{i}})}^{2}}}}{N} \right]}^{0.5}}, $ (8)

$MRE=\frac{100}{N}\sum\limits_{i=1}^{N}{\left| \frac{{{O}_{i}}-{{S}_{i}}}{{{O}_{i}}} \right|}, $ (9)

${{d}_{IA}}=1-\frac{\sum\nolimits_{i=1}^{N}{{{({{O}_{i}}-{{S}_{i}})}^{2}}}}{\sum\nolimits_{i=1}^{N}{{{(\left| {{S}_{i}}-\overline{O} \right|+\left| {{O}_{i}}-\overline{O} \right|)}^{2}}}}, $ (10)

where S_i and O_i are the simulated and observed values, respectively; N is the number of simulated values; and $\overline O$ is the mean observed value. The larger R² and d_IA values and the smaller MAE and RMSE values indicate the higher performance of the model.

In the solar greenhouse, about 81% of the total root length density of tomato plants under furrow irrigation was concentrated in the 0-50 cm soil layers. This value differs from that under drip irrigation, under which roots were mainly concentrated in the top soil layer because of high irrigation frequencies and low irrigation amounts. For example, Zotarelli et al. (2009) found that under drip irrigation, 70%-75% of the total root length density of tomato plants was concentrated in the 0-15 cm soil layers. Except for irrigation methods, soil texture and soil bulk density may also affect the root length density distribution (Dexter, 2004; Zotarelli et al., 2009). High soil clay content and high soil bulk density exhibit negative effects on root growth, while low soil clay content and low soil bulk density have positive effects on root growth (Oliveira et al., 1996; Dexter, 2004; Zotarelli et al., 2009). In this study, the low soil clay content (12.6%) and moderate soil bulk density (1.46 g/cm³) seem to have promoted root growth of tomato plants.

We found an exponential relationship between relative root length density and relative root depth of tomato plants (Eq. 11), being similar to the findings for other plants such as apple trees (Yao, 2004) and grape vines (Zhou, 2007):

${{L}_{r}}(Z)=1.2567{{\text{e}}^{-2.294{{Z}_{r}}}}\ \ (n=8, R^2=0.99, P< 0.001), $ (11)

where L_r(Z) is the relative root length density of tomato plants, which can be obtained from L_r(Z)=L(Z)/L_max with L(Z) being the root length density (cm/cm³) and L_max being the maximum root length density (cm/cm³; average value of 0.2371 cm/cm³ for the three selected tomato plants); and Z_r is the relative root depth, which can be obtained fromZ_r=z/z_m with zbeing the root depth (cm) and z_m being the maximum root depth (100 cm).

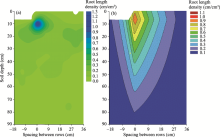
Figure 3 shows the root length density distribution of tomato plants within and between rows under furrow irrigation, with (0, 0) being the origin position of each plant. Generally, the root length density distributions of tomato plants are similar when the distances from the origin position are more or less the same. The root length density distributions of tomato plants under furrow irrigation were concentrated horizontally within distances of 0-18 cm from the origin position to the furrow side, 0-30 cm from the origin position to the bed side, and 0-18 cm from the origin position within the same row. The root length density of tomato plants decreased as the horizontal distance from the origin position increased. The range of horizontal distribution of root length density on the bed side was greater than that on the furrow side because of large plant spacing. There were exponential relationships of relative root length density (L_r(Z)) with both relative furrow side distance (R_F) and relative bed side distance (R_B):

${{L}_{r}}({{Z}_{F}})=0.8923{{\text{e}}^{-0.771{{R}_{F}}}}\ \ \ \ (n=4, R2=0.84, P< 0.10)$, (12)

${{L}_{r}}({{Z}_{B}})=0.7656{{\text{e}}^{-0.777{{R}_{B}}}}\ \ \ \ (n=7, R2=0.73, P< 0.05)$, (13)

where R_F is the relative furrow side distance, which can be obtained from R_F=r_F/r_Fm, with r_F being the distance from the origin position of tomato plant to the furrow side (cm) and r_Fm being the maximum distance from the origin position of tomato plant to the furrow side (21 cm); andR_B is the relative bed side distance, which can be obtained from R_B=r_B/r_Bm, with r_B being the distance from the origin position of tomato plant to the bed side (cm) and r_Bm being the maximum distance from the origin position of tomato plant to the bed side (39 cm).

Figure 3 also clearly shows an approximate axial symmetry in the horizontal distribution of root length density with respect to distance from the origin position. The average root length density at the same sampling depth and radial distance within the root zone of the three selected tomato plants was used for simulating the two-dimensional depth and radial distribution. As described above, there are exponential relationships between relative root length density and distance from the origin position in the both vertical and horizontal directions. Thus, the two-dimensional root length density of tomato plants used in the HYDRUS-2D model (Vrugt et al., 2001a; Š imů nek et al., 2006) could be estimated as follows:

$\beta (r, z)=(1-z/{{z}_{m}})(1-{{r}_{B}}/{{r}_{Bm}}){{\exp }^{-\left( \frac{{{p}_{z}}}{{{z}_{m}}}\left| {{Z}^{*}}-z \right|+\frac{{{p}_{r}}}{{{r}_{Bm}}}\left| {{R}^{*}}-{{r}_{B}} \right| \right)}}, $ (14)

where β (r, z) is the dimensionless two-dimensional spatial distribution of root water uptake; and p_z, p_r, Z^* and R^* are the empirical coefficients, which can represent the asymmetrical root water uptake with radius and depth to allow for the maximum root water uptake at any depth (Vrugt et al., 2001a; Zhou et al., 2007). The empirical coefficients of Z^* and R^* shown in Table 2 indicate that the maximum root length density was at a depth of 10 cm and at the origin of the plant, being consistent with the observed values (Fig. 4a). The simulated two-dimensional root length density used in the HYDRUS-2D model is shown in Figure 4b. There was a significant relationship between observed and simulated two-dimensional root length density values (R²=0.57, P< 0.001).

Fig. 3

	Figure Option ViewDownloadNew Window
	Fig. 3 Horizontal distribution of root length density of tomato plants under furrow irrigation based on soil sampling

Table 2

Table 2

Table 2 Parameter values of two-dimensional root length density used in the root water uptake function pz pr Z* (cm) R* (cm) 2.89 6.08 10 0

Table 2 Parameter values of two-dimensional root length density used in the root water uptake function

Fig. 4

	Figure Option ViewDownloadNew Window
	Fig. 4 Observed (a) and simulated (b) two-dimensional root length density values of tomato plants

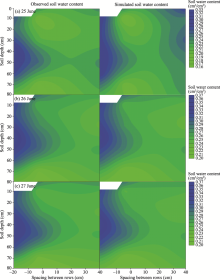
Overall, differences of soil water content at different positions in the upper soil layers (0-40 cm) were larger than those in the deeper soil layers (40-80 cm). This may be due to that the upper soil layers are more directly affected by evapotranspiration and irrigation. After each irrigation event, soil water content increased rapidly in the upper soil layers (0-40 cm), especially in the top layer (0-20 cm), and the increases mainly occurred in the center and at the edge of the furrow (Fig. 5). The difference of soil water content between the edge of the furrow and the center of the bed in the 40-80 cm soil layers was negligibly small because the strictly controlled irrigation limited water infiltration to a particular soil depth.

Fig. 5

	Figure Option ViewDownloadNew Window
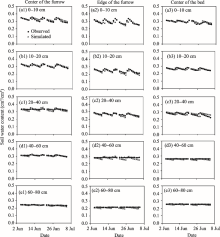	Fig. 5 Comparison of observed and simulated soil water content values at different locations (i.e., center of the furrow, edge of the furrow and center of the bed) and different soil depths

In this study, we used the HYDRUS-2D model to simulate soil water content at different locations and depths. Soil water content values simulated by the HYDRUS-2D model were compared with those observed by the ECH₂O sensors (Fig. 5). It can be seen that the simulated values generally agreed well with the observed values both spatially and temporally, except for some values at deeper soil layers, e.g., 40-60 cm soil layer at the edge of the furrow. The simulation errors were small, with RMSE ranging from 0.006 to 0.020 cm³/cm³, MAEvarying from 0.005 to 0.018 cm³/cm³, and MRE less than 7% (Table 3). It should be noted that the errors were slightly larger at the edge of the furrow and in the 20-40 cm soil layer in the bed. The differences between observed and simulated values may be attributed to the following reasons. Root length density distribution influences root water uptake and in turn affects soil water content. The accuracy of estimation of root length density also has a direct effect on the simulation of soil water content (Zhou et al., 2007). In this study, the differences between observed and estimated root length density distributions (see Fig. 4) may lead to a subsequent exaggeration of the differences between observed and estimated values in root water uptake, and the exaggerated differences in turn affect the simulation of soil water content in the deeper soil layers. Root water uptake depends not only on the root length density distribution but also on soil water availability (Vrugt et al., 2001b). Strictly controlled irrigation limited the available water and water infiltration to deeper soil layers especially at the edge of the furrow and the center of the bed and thus affected root water uptake and soil water content in the deeper soil layers.

Table 3

Table 3

Table 3 Simulation error analyses of soil water content at different locations (i.e., center of the furrow, edge of the furrow and center of the bed) and different soil depths Soil depth (cm) Error parameter Location Center of the furrow Edge of the furrow Center of the bed 0-10 RMSE(cm3/cm3) 0.014 0.019 0.011 MAE(cm3/cm3) 0.012 0.013 0.008 MRE(%) 3.7 4.2 2.8 10-20 RMSE(cm3/cm3) 0.009 0.014 0.010 MAE(cm3/cm3) 0.008 0.011 0.007 MRE(%) 2.7 4.8 2.5 20-40 RMSE(cm3/cm3) 0.015 0.011 0.020 MAE(cm3/cm3) 0.013 0.009 0.018 MRE(%) 4.0 3.6 6.9 40-60 RMSE(cm3/cm3) 0.007 0.018 0.010 MAE(cm3/cm3) 0.005 0.016 0.007 MRE(%) 1.6 5.6 2.8 60-80 RMSE(cm3/cm3) 0.006 0.011 0.007 MAE(cm3/cm3) 0.005 0.009 0.005 MRE(%) 2.2 4.2 2.0 Note: RMSE, root mean square error; MAE, mean absolute error; MRE, mean relative error.

Table 3 Simulation error analyses of soil water content at different locations (i.e., center of the furrow, edge of the furrow and center of the bed) and different soil depths

Table 4 shows the statistical indicators of goodness of fit for the HYDRUS-2D model at different locations, i.e., center of the furrow, edge of the furrow and center of the bed. Regression coefficient (b) and coefficient of determination (R²) ranged from 0.967 to 0.997 and 0.58 to 0.91 (P< 0.001) at the three locations, respectively, indicating that most of the total variance of the observed values could be explained by the HYDRUS-2D model. Simulation errors were all small at each one of locations, with RMSEof 0.011-0.015 cm³/cm³, MAE of 0.009-0.012 cm³/cm³, and MRE of 2.8%-4.5%. Values of d_IA ranged from 0.88 to 0.98, indicating that the mean square error is close to the potential error. Based on these results, we conclude that soil water contents simulated by the HYDRUS-2D model fitted well with those observed by the ECH₂O sensors. Therefore, the HYDRUS-2D model is suitable for simulating soil water distribution in a furrow irrigation system. Furthermore, the performance of the HYDRUS-2D model in our study was slightly better than that in other studies (Crevoisier et al., 2008; Ebrahimian et al., 2012). For instance, Ebrahimian et al. (2012) used a HYDRUS-2D model to simulate soil water content and the result showed that the R² values for both fixed and variable alternate furrow irrigation treatments and for conventional furrow irrigation treatments were in the range of 0.571 to 0.878 with standard errors ranging from 0.089 to 0.096 cm³/cm³. The better performance of the HYDRUS-2D model in our study may be due to a full consideration of root water uptake in the model.

Table 4

Table 4

Table 4 Statistical indicators of goodness of fit for the HYDRUS-2D model at different locations (i.e., center of the furrow, edge of the furrow and center of the bed) Location b R2 RMSE (cm3/cm3) MAE (cm3/cm3) MRE(%) dIA Center of the furrow 0.997 0.91 0.011 0.009 2.8 0.98 Edge of the furrow 0.967 0.86 0.015 0.012 4.5 0.94 Center of the bed 0.996 0.58 0.012 0.009 3.4 0.88 Average 0.988 0.89 0.013 0.010 3.6 0.97 Note: b, regression coefficient; R2, coefficient of determination; RMSE, root mean square error; MAE, mean absolute error; MRE, mean relative error; dIA, index of agreement.

Table 4 Statistical indicators of goodness of fit for the HYDRUS-2D model at different locations (i.e., center of the furrow, edge of the furrow and center of the bed)

The observed and simulated two-dimensional soil water contents during an irrigation event are shown in Figure 6. Soil water content values simulated by the HYDRUS-2D model well matched with those observed by the ECH₂O sensors before irrigation, during the day of irrigation, and after irrigation. The values ofb, R², RMSE, MAE and d_IA ranged from 0.960 to 1.015, 0.74 to 0.85, 0.016 to 0.020 cm³/cm³, 0.012 to 0.018 cm³/cm³ and 0.994 to 0.997, respectively (Table 5).

Fig. 6

	Figure Option ViewDownloadNew Window
	Fig. 6 Comparison of observed (left column) and simulated (right column) two-dimensional soil water content values on (a) 25 June (before irrigation), (b) 26 June (during the day of irrigation), and (c) 27 June (after irrigation)

Table 5

Table 5

Table 5 Statistical indicators of goodness of fit for the HYDRUS-2D model during an irrigation event (i.e., before irrigation, during the day of irrigation, and after irrigation) Date b R2 RMSE(cm3/cm3) MAE(cm3/cm3) dIA 25 June (before irrigation) 0.960 0.77 0.020 0.016 0.994 26 June (during the day of irrigation) 1.015 0.85 0.016 0.018 0.997 27 June (after irrigation) 1.008 0.74 0.020 0.012 0.996 Note: b, regression coefficient; R2, coefficient of determination; RMSE, root mean square error; MAE, mean absolute error; dIA, index of agreement.

Table 5 Statistical indicators of goodness of fit for the HYDRUS-2D model during an irrigation event (i.e., before irrigation, during the day of irrigation, and after irrigation)

Relationships of irrigation amount (I) with irrigation interval (Q) and deep percolation amount (D) under different daily average potential transpiration rate (T_p) values for no water-stress cases are shown in Figure 7. The trends of the Q-I-D relationship were as follows: (1) at the same value of I, Q with a low daily average T_p was higher than Q with a high daily average T_p; (2) at the same value of Q, both I and D with a low daily average T_p were lower than I and D with a high daily average T_p; (3) under daily average T_p values of 1.5, 2.7 and 4.0 mm/d, D began to appear when I was greater than 28, 31 and 34 mm, respectively, and the corresponding Q values were 17, 9 and 6 days. Q increased rapidly as I increased up to 60 mm, afterwards there was only a small increase in Q when I was greater than 60 mm. This indicates that most of the increase in I became an increase in D. Under daily average T_p values of 1.5, 2.7 and 4.0 mm/d, Q values were 25, 13 and 8 days, respectively when I was 60 mm. However, under the same daily average values of T_p, the maximum Q values were 29, 17 and 11 days, respectively.

Fig. 7

	Figure Option ViewDownloadNew Window
	Fig. 7 Relationships (a) between irrigation amount and irrigation interval and (b) between irrigation amount and deep percolation amount under different daily average potential transpiration rate (Tp) values

When the priority was to limit water use, the maximum I values were no more than 28 and 34 mm and the corresponding Q values were less than 17 and 6 days for lower daily average T_p (1.5 mm/d) and higher daily average T_p (4.0 mm/d), respectively. When the priority was to limit the irrigation frequency, I was 60 mm and the corresponding Q values were no more than 25 and 13 days for lower daily average T_p (1.5 mm/d) and higher daily average T_p (4.0 mm/d), respectively. Furthermore, the corresponding D values were 10%-18% of I.

The result of high irrigation frequency with a low amount of water for each irrigation event in this study was close to that in our previous study (Qiu, 2014). Actually, infrequent irrigation with a large amount of water for each irrigation event approximates the practice of local farmers. However, this irrigation method results in 10%-18% of the irrigation water loss. Therefore, infrequent irrigation with a large amount of water for each irrigation event is not recommended for arid regions.