Cite this Article
WANG Tongtong, Catherine E STEWART, MA Jiangbo, ZHENG Jiyong, ZHANG Xingchang. , Applicability of five models to simulate water infiltration into soil with added biochar. Journal of Arid Land, 2017, 9(5): 701-711.  
Permissions
Copyright © 2017, Editorial office of Journal of Arid Land
All right reserved
Received:2016-09-06 Revised:2017-06-28
Applicability of five models to simulate water infiltration into soil with added biochar
WANG Tongtong1,2, Catherine E STEWART3, MA Jiangbo1,2, ZHENG Jiyong1,*, ZHANG Xingchang1
1 State Key Laboratory of Soil Erosion and Dryland Farming on the Loess Plateau, Institute of Soil and Water Conservation, Northwest A&F University, Yangling 712100, China
2College of Natural Resources and Environment, Northwest A&F University, Yangling 712100, China
3Soil-Plant-Nutrient Research Unit, United States Department of Agriculture-Agricultural Research Service, Fort Collins CO 80526-8119, USA
*Corresponding author: ZHENG Jiyong (E-mail: zhjy@ms.iswc.ac.cn)
Abstract

As a soil amendment, biochar can reduce soil bulk density, increase soil porosity, and alter soil aggregates and thus affect the infiltration. Researchers have proposed and revised several theoretical models to describe the process of soil infiltration. Although these models have been successfully used to evaluate the soil infiltration in different scenarios in agricultural fields, little effort has been devoted to assess their performances in arid and semi-arid soils after the addition of biochar. A laboratory experiment was performed to study the infiltration characteristics of two typical Loess Plateau soils at three particle sizes (2-1, 1-0.25, and <0.25 mm) and five biochar application amounts (0, 10, 50, 100, and 150 g/kg). The performance of five models (i.e., the Philip model, Kostiakov model, Mezencev model, USDA-NRCS model, and Horton model) in simulating the infiltration process was then evaluated based on the adjusted coefficient of determination and a reduced Chi-Square test. Results indicated that the Horton model best simulated the water-infiltration process in an aeolian sandy soil with added biochar. However, the Mezencev model best simulated the infiltration process in a loamy clay soil (Eum-Orthic Anthrosol). The three-parameter model, i.e., Mezencev and Horton models can better describe the relationship between cumulative infiltration and infiltration time. In conclusion, biochar reduced the soil infiltration capacity of the aeolian sandy soil and increased that of the Eum-Orthic Anthrosol.

Key words: infiltration models; biochar; Horton model; Mezencev model; Loess Plateau
1 Introduction

Biochar is a carbon-rich product of the thermal decomposition of organic material under limited oxygen supply at a certain temperature (< 700° C) (Chen et al., 2010; Wang et al., 2017). The application of biochar as a soil amendment or a slow-release fertilizer carrier or for carbon sequestration has recently attracted noticeable attentions (Marris, 2006; Lehmann, 2007; Agegnehu et al., 2015). The addition of biochar inevitably alters the physical and chemical properties of soil (Liu et al., 2012; Herath et al., 2013), thereby affecting soil water infiltration. Agegnehu et al. (2015) reported that biochar application improved soil organic carbon, soil water content, soil nutrient status, and peanut yield. Moreover, the potential of biochar addition to improve soil fertility and water-holding capacity has been widely recognized (Asai et al., 2009; Lehmann and Joseph, 2009; Zheng et al., 2012; Akhtar et al., 2014).

Infiltration is the physical process by which water descends from the surface into the soil, and it is an essential part of the transformation of water from precipitation to surface water, soil water, and groundwater (Hillel, 1998; Zhao and Wu, 2004). Infiltration not only controls the entry of water into the soil and the depth of penetration into the groundwater via soil moisture redistribution but also determines the timing and quantity of the runoff (Moore et al., 1981). The study of soil water infiltration can provide a scientific basis for evaluating the surface and groundwater resources and also for determining the needed irrigation parameters (Li et al., 2009).

Researchers have proposed and revised several theoretical models to describe the process of soil infiltration (Al-Azawi, 1985; Mao et al., 2011). These models include the Green-Ampt model, the Philip model, the Kostiakov model, the Horton model, the Kostiakov-Lewis (Mezencev) model, and the United States Department of Agriculture-Natural Resources Conservation Service (USDA-NRCS) model (Mishra et al., 2003; Parhi et al., 2007; Rashidi and Seyfi, 2007). Although these models have been successfully used to evaluate and compare soil infiltration in different scenarios in agricultural fields (Dashtaki et al., 2009; Valiantzas, 2010; Duan et al., 2011), little effort has been devoted to assess their performances in arid and semi-arid soils after the addition of biochar. Therefore, we investigated soil water infiltration in two typical soil types (Eum-Orthic Anthrosol and aeolian sandy soil) of the Loess Plateau at five different biochar addition amount (0, 10, 50, 100, and 150 g/kg) and three size fractions (2-1 mm, 1-0.25 mm, and < 0.25 mm) via soil column simulation experiments in the laboratory. Furthermore, the performances of the Philip model, Kostiakov model, Mezencev model, USDA-NRCS model, and Horton model were compared by evaluating the fitting parameters and model errors. The main objectives of this study were to verify the model applicability and to assess the performance of these infiltration models for arid and semi-arid soils with added biochar.

2 Materials and methods
2.1 Soil collection and biochar preparation

We selected a Eum-Orthic Anthrosol from the southern Loess Plateau and an aeolian sandy soil from the northern Loess Plateau as the experimental soils. The Eum-Orthic Anthrosol was collected from a plot at the Institute of Soil and Water Conservation (ISWC) of the Chinese Academy of Sciences (CAS) in Yangling District, Shaanxi Province, and the aeolian sandy soil was obtained from a forest land in the Liudaogou Watershed in Shenmu County, Shaanxi Province. The soils were collected from 0-20 cm layer, and visible roots and organic residue were hand-removed. Subsequently, the soils were air-dried and sieved through a 2-mm sieve, and the soil bulk density was measured in the vicinity of each sampling site using the cutting ring method. Air-dried soil was sieved to obtain the < 1-mm fraction, and the soil mechanical components were measured using a laser particle size analyzer (MS-2000, Malvern Instruments Ltd., Malvern, UK). The basic physical properties of the two soil types are shown in Table 1.

Table 1 Physical properties of the two experimental soils

Biochar was derived from a mixed tree’ s residuals including poplar, elm, pagoda tree, and apple tree. It was produced through a fast pyrolysis process (550° C) by YIXIN Bioenergy Technology Co. Ltd. in Yangling District, Shaanxi Province, China. The carbon content of the biochar was 83.24% (± 2.36%) as determined by dry combustion at 800° C with a bulk density of 0.58 g/cm3. The biochar was sealed in airtight plastic bags after being sieved into three size fractions (2-1, 1-0.25, and < 0.25 mm).

2.2 Experimental design

Three size fractions (2-1, 1-0.25, and < 0.25 mm) of biochar were uniformly mixed with aeolian sandy soil and Eum-Orthic Anthrosol at five concentrations (0, 10, 50, 100, and 150 g/kg soil).

2.3 Infiltration experiment

A specially designed polyvinyl chloride (PVC) pot with an inner diameter of 5 cm and a height of 50 cm was used to measure soil infiltration. The bottom of the pot was covered with a layer of fine gauze to prevent the loss of soil particles. The inner surface of the pot was treated with a thin layer of vaseline to reduce the effect of the wall on infiltration. All of the pots were packed with the required amount of soil (the depth of the soil packed in the flume was 30 cm) to achieve field bulk densities of 1.48 g/cm3 for the Eum-Orthic Anthrosol and 1.56 g/cm3 for the aeolian sandy soil. The soil column was loaded uniformly in every 5-cm layers. The packed soil surface of each layer was roughened before the next layer was added to prevent discontinuity.

The soil column was vertically fixed and water was provided using the Markov bottle. The water head was fixed at 3 cm. The valve was opened to wet the soil surface at the start time and the infiltration was continuously recorded. When the wetting front had moved through three-quarters of the column, the valve was shut down to stop the water supply.

2.4 Models and data analysis

2.4.1 Infiltration models

Because cumulative infiltration can be easily measured during the water-infiltration process, cumulative infiltration and infiltration time were selected for the curve-fitting analysis (Liu et al., 2011; Parchami-Araghi et al., 2013). Several theory-based approximate and empirical models that simplify the concepts involved in the infiltration process have been developed for field applications (Table 2). The effects of biochar addition on the infiltration characteristics of soil were studied using these models.

Table 2 Models of soil water infi ltration

According to Liu et al. (2010), an implicit functional relationship between cumulative infiltration and infiltration time exists in the Green and Ampt model and should be reflected in the infiltration equation, but this process may introduce new parameters into the adjustment equation and may cause errors. Therefore, the Philip model was the only theory-based model selected for this study.

2.4.2 Model evaluation and data analysis

The model parameters were estimated using a dynamic curve-fitting tool in OriginPro software for Windows version 8.5.1 SR2 and were used to compare the measured data and the curve fittings among different conditions (two soil types with different sizes and different amounts of added biochar). This approach can achieve the best model fitting while minimizing the sum of the squared error. The estimated parameters and fitting procedure for all five infiltration models studied here were analysed with one-way analysis of variance (ANOVA) using OriginPro software. A one-way ANOVA was conducted to compare the means of the estimated parameters associated with the five models at P< 0.05 level for each soil type. The accuracies of the infiltration models were evaluated by comparing the measured and the predicted infiltration values. The statistically adjusted coefficient of determination (Adj-R2), reduced Chi-Sqr and standard error (SE) values were used to evaluate the models.

All of the selected soil-infiltration models were nonlinear. Therefore, the Adj-R2 was used instead of the coefficient of determination (R2), and consideration was given to the results of the extra variables. The Adj-R2and R2 have the same statistical significance, and thus, when R2 is close to 1, the relationship between the independent variable and the dependent variables will achieve a higher degree of curve fitting (Van de Genachte et al., 1996).

The reduced Chi-Sqr is equivalent to the residual sum of squares of the one-way ANOVA. This value is actually the error between the fitted values and the actual values and smaller values indicate stronger degrees of curve fitting. Typically, the reduced Chi-Sqr value is larger than zero. But, for perfect goodness of fit, the reduced Chi-Sqr value must be close to or equal to zero. Therefore, all of the observed cumulative infiltration values should be close to or exactly the same as the model-predicted ones.

$R^2=1-\frac{RSS}{TSS}$ (1)

$Adj-R^2:\ \ \ {\overline R}^2=1-\frac{RSS/dfE}{TSS/dfE}$, (2)

$ Reduced \ Chi-Sqr:\ Reduced \ \ \ x^2=\frac{x^2}{dfE}=\frac{RSS}{dfE}$, (3)

where RSS is the residual sum of squares; TSS is the total sum of squares; and dfE is the error degrees of freedom.

The SE characterizes the discreteness between the accuracy of the measured values and the predicted values. In general, small SE values indicate that the fitting value is close to the true value. Finally, the Adj-R2 and reduced Chi-Sqr values were calculated to compare model performance, and the SE was calculated to evaluate the model parameters.

3 Results
3.1 Model parameters

A comparative analysis of the soil water-infiltration characteristics for the two soil types at different particle sizes and amounts of added biochar was conducted. The estimated parameter values for the five selected infiltration models are listed in Tables 3 and 4. It can be seen that for the five infiltration models from the same experimental treatment, in both the aeolian sandy soil and the Eum-Orthic Anthrosol, the values of k, b, K′ and a″ were very similar. These empirical parameters had somewhat similar soil physical meanings with the theoretical basis of the Philip model’ s S value (sorptivity). A size comparison of each of the model parameters indicated that the k and K′ values were larger than the a″ values. In addition, the results were similar to those reported by Dashtaki et al. (2009). Researchers presumed that the values of Philip’ s A, Mezencev’ s A′ and Horton’ s a were close to the measured infiltration rate. However, these values were not equal and no obvious relationship between these values and the measured infiltration rates was found (Dashtaki et al., 2009). Dashtaki et al. (2009) attributed this phenomenon to the fact that these parameters are intrinsically empirical.

Table 3 Estimated parameters of the five evaluated soil infiltration models for the aeolian sandy soil
Table 4 Estimated parameters of the five evaluated soil infiltration models for the Eum-Orthic Anthrosol

Tables 5 and 6 show that for the different experimental treatments, each infiltration model yielded the same Kostiakov model k values for the aeolian sandy soil of the same particle size. Tables 5 and 6 also show that that these k values tended to decrease as the amount of added biochar increased. The k value reflects the decrease in the infiltration rate over time, where larger k values correspond to faster decreases (Mishra et al., 2003). The addition of biochar can effectively reduce the infiltration capacity of the aeolian sandy soil. However, infiltration in the Eum-Orthic Anthrosol differed from that in the aeolian sandy soil. For the same size of biochar, the k values showed an increasing trend as the amount of added biochar increased. Additionally, the application of biochar increased the infiltration capacity of the Eum-Orthic Anthrosol. These results are similar to those reported by Gao et al. (2011) and Qi et al. (2014). The n value is an index representing the infiltration characteristics (Shukla et al., 2003). The aeolian sandy soil and the Eum-Orthic Anthrosol showed little variation in n. For the Philip model, at the same size of biochar, the S and A values for the aeolian sandy soil increased as the amount of added biochar increased, whereas those for the Eum-Orthic Anthrosol did not change significantly. At the same amount of added biochar, the S and A values for the aeolian sandy soil and the Eum-Orthic Anthrosol did not exhibit a consistent pattern over different sizes of biochar.

Table 5 Standard errors of the estimated parameters of the five soil-infiltration models for the aeolian sandy soil
Table 6 Standard errors of the estimated parameters of the five soil-infiltration models for the Eum-Orthic Anthrosol

Regarding the Horton model, because a and Philip A values had the same physical significance, their change trends were similar over the various sizes and amounts of added biochar. Additionally, the cand Kostiakov n are both infiltration characteristic indices. Their change trends were thus similar and indirectly indicated that the fitting accuracy of the model was satisfactory. The K′ and b′ parameters of the Mezencev model and the a″ and b″ parameters of the NRCS model were all dimensionless empirical constants and did not change consistently. The k and Svalues and the A and a values for the aeolian sandy soil were larger than those for the Eum-Orthic Anthrosol under the same experimental conditions. These results indicate that the sorptivity and saturated hydraulic conductivity were higher for the aeolian sandy soil than for the Eum-Orthic Anthrosol.

3.2 Model performance

Tables 7 and 8 present the Adj-R2 and reduced Chi-Sqr values for the five infiltration models. Adj-R2values of the five infiltration models exceeded 0.9 for every experimental treatment, indicating the perfect performance of these models. The Adj-R2 and reduced Chi-Sqr values indicated that the Horton and Mezencev models were the most appropriate.

Table 7 Reduced Chi-Sqr and Adj-R2values of the five evaluated soil infiltration models for the aeolian sandy soil
Table 8 Reduced Chi-Sqr and Adj-R2values of the five evaluated soil infiltration models for the Eum-Orthic Anthrosol

For the aeolian sandy soil, the Horton model exhibited the best performance except for the experimental treatment in which < 0.25-mm biochar was added at 150 g/kg; in the latter case, the Mezencev model was better. For the Eum-Orthic Anthrosol, the Mezencev model had the best performance with exception of the control treatment and the experimental treatment in which1-2-mm biochar was added at 150 g/kg. For the exception, the Horton model was better. In ddition, whether the aeolian sandy soil or Eum-Orthic Anthrosol soil, both in the control treatment, the optimal infiltration model was the Horton model. When the biochar added level reached < 0.25 mm and 150 g/kg, the optimal model was Mezencev model. It mean that different amounts of biochar addition were correspondent with different the optimal infiltration models under these two soil types.

4 Discussion
4.1 Optimal infiltration models

Up to now, few studies have investigated the effects of applied biochar on the soil water infiltration characteristics. Duan et al. (2011) studied the soil water infiltration properties of three types of turf soil with healthy grass growing under field conditions and found that the Horton and Mezencev models were the best performing infiltration models. Dashtaki et al. (2009) investigated the site-dependence performance of the Kostiakov, Philip, Horton and Mezencev models at 123 sites with different soil series in Iran and found that the top two infiltration models were the Mezencev and Horton models. In our study, the three-parameter models, i.e., the Mezencev and Hortan models, optimally described the relationship between cumulative infiltration and infiltration time in the Loess Plateau soils with added biochar, being consistent results with Dashtaki et al. (2009) and Duan et al. (2011). Although the two-parameter models (i.e., Philip, Kostiakov and USDA-NRCS models) could also simulate the relationship, the simulations were not as accurate as the three-parameter models, because the additional parameter in the three-parameter model is primarily included to adjust the model and to improve its accuracy by increasing the model’ s stability and decreasing the disturbance and deviation. Shukla et al. (2003) also found that three-parameter models provided the best fit to observed infiltration and best predicted the capacity for cumulative infiltration.

However, with the increasing amount of biochar, the Mezencev model performed better than the Hortan model. This trend was name as “ Model Replacement” . We speculated that it is probably related to the empirical constants of the model. In other word, in Horton model, there is only one empirical constant c. However, in Mezencev model, there are two empirical constants K′ and b′ . Biochar, as a soil amendment, is not intrinsic in the soil, more empirical parameters may be needed to correct the optimal infiltration model, and it is more suitable for modelling the real environmental conditions. Moreover, this difference among the optimum models may be attributable to the effects of biochar size and amount in the two soil types. Admittedly, the factors causing the “ Model Replacement” phenomenon of the optimal model require further study.

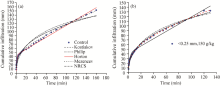
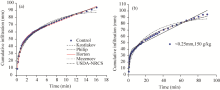
4.2 Effect of biochar on soil water infiltration characteristics by model analysis

In this study, the best fitting models of the infiltration process differed between the two soil types. However, in order to display the measured and fitted infiltration curves, we chose the control treatment and < 0.25-mm biochar at 150 g/kg treatment as the representatives (Figs. 1 and 2). Figure 1a and Figure 1b showed that under the control treatment, a cumulative infiltration of 95 mm required approximately 16 min in the aeolian sandy soil. In contrast, 90 min was required for the same infiltration amount in the treatment with biochar. Obviously, the application of biochar reduced the infiltration capacity of the aeolian sandy soil. On the contrary, Figure 2a and Figure 2b showed that under the control treatment, approximately 50 min were required to achieve a cumulative infiltration of 80 mm, whereas when the optimum biochar amount and size were added to the Eum-Orthic Anthrosol, 40 min were required. Therefore, it is clear that the application of biochar can increase the infiltration capacity of the Eum-Orthic Anthrosol. These results are consistent with the obtained fitting parameters. Brodowski et al. (2006) suggested that the main reasons of this phenomenon are the porous structure and the functional groups on the surface of the biochar. Initially, the effects of adding biochar on the soil moisture are mainly attributable to changes in the soil pore structure. But, during the later stages of infiltration, the important factors include micro-aggregation of the biochar and the chemical absorbance caused by the oxidized functional groups. In addition, the comparison between Figure 1 and Figure 2 suggested that regardless of the amount of added biochar, the infiltration rate at any infiltration time in the Eum-Orthic Anthrosol was much lower than in the aeolian sandy soil. Based on the results in Table 1, we attributed this difference in infiltration to the differences in soil texture: sticky texture of the Eum-Orthic Anthrosol and lighter texture of the aeolian sandy soil (Qi et al., 2014). Moreover, other soil physical factors, such as the soil structure, porosity and moisture content, may also affect the infiltration process (Yan et al. 2013).

Fig. 1 A comparison of the measured and fitted infiltration curves for the aeolian sandy soil. (a) Control; (b) < 0.25-mm biochar at 150 g/kg.

Fig. 2 A comparison of the measured and fitted infiltration curves for the Eum-Orthic Anthrosol. (a) Control; (b) < 0.25-mm biochar at 150 g/kg.

5 Conclusions

This study evaluated the performance of five classical infiltration models in simulating soil water infiltration in an aeolian sandy soil and a Eum-Orthic Anthrosol with added biochar. The investigated models included a theory-based model, the Philip model, and four empirical models: the Kostiakov model, the Mezencev model, the NRCS model, and the Horton model. The results indicated that the five infiltration models all fit the data well. However, the optimal infiltration model under different amounts of added biochar of different particle sizes for the aeolian sandy soil and the Eum-Orthic Anthrosol was the Horton model and the Mezencev model, respectively. Overall, the Mezencev and Horton models performed better than the other three infiltration models according to various validation indices, including the Adj-R2 and reduced Chi-Sqr. As the amount of added biochar increased and as biochar size decreased, the best model shifted from the Horton model to the Mezencev model. The results indicated that the three-parameter model can better describe the relationship between cumulative infiltration and infiltration time. In conclusion, the addition of biochar reduced the infiltration capacity of an aeolian sandy soil and increased that of a Eum-Orthic Anthrosol.

Acknowledgements

This research was supported by the National Natural Science Foundation of China (41571225) and the National Key Research and Development Program of China (2016YFC0501702, 2015BAC01B01).

The authors have declared that no competing interests exist.

Reference
[1] Agegnehu G, Bass A M, Nelson P N, et al. 2015. Biochar and biochar-compost as soil amendments: effects on peanut yield, soil properties and greenhouse gas emissions in tropical North Queensland , Australia. Agriculture, Ecosystems & Environment, 213: 72-85. [Cited Within:1]
[2] Akhtar S S, Li G T, Andersen M N, et al. 2014. Biochar enhances yield and quality of tomato under reduced irrigation. Agricultural Water Management, 138: 37-44. [Cited Within:1]
[3] Al-Azawi S A. 1985. Experimental evaluation of infiltration models. Journal of Hydrology, 24(2): 77-88. [Cited Within:1]
[4] Asai H, Samson B K, Stephan H M, et al. 2009. Biochar amendment techniques for upland rice production in Northern Laos: 1. Soil physical properties, leaf SPAD and grain yield. Field Crops Research, 111(1-2): 81-84. [Cited Within:1]
[5] Brodowski S, John B, Flessa H, et al. 2006. Aggregate-occluded black carbon in soil. European Journal of Soil Science, 57(4): 539-546. [Cited Within:1]
[6] Chen Y, Shinogi Y, Taira M. 2010. Influence of biochar use on sugarcane growth, soil parameters, and groundwater quality. Australian Journal of Soil Research, 48(7): 526-530. [Cited Within:1]
[7] Dashtaki S G, Homaee M, Mahdian M H, et al. 2009. Site-dependence performance of infiltration models. Water Resources Management, 23(13): 2777-2790. [Cited Within:4]
[8] Duan R B, Fedler C B, Borrelli J. 2011. Field evaluation of infiltration models in lawn soils. Irrigation Science, 29(5): 379-389. [Cited Within:3]
[9] Gao H Y, He X S, Geng Z C, et al. 2011. Effects of biochar and biochar-based nitrogen fertilizer on soil water-holding capacity. Chinese Agricultural Science Bulletin, 27(24): 207-213. (in Chinese). [Cited Within:1]
[10] Green W H, Ampt G A. 1911. Studies of soil physics. The Journal of Agricultural Science, 4(1): 1-24. [Cited Within:1]
[11] Herath H M S K, Camps-Arbestain M, Hedley M. 2013. Effect of biochar on soil physical properties in two contrasting soils: An Alfisol and an Andisol. Geoderma, 210: 188-197. [Cited Within:1]
[12] Hillel D. 1998. Environmental Soil Physics: Fundamentals, Applications, and Environmental Considerations. San Diego: Academic Press, 56-64. [Cited Within:1]
[13] Horton R E. 1940. An approach towards a physical interpretation of infiltration capacity. Proceedings of Soil Science Society of America Journal, 5: 399-417. [Cited Within:1]
[14] Kostiakov A N. 1932. On the dynamics of the coefficient of water percolation in soils and on the necessity of studying it from a dynamic point of view for purpose of amelioration. In: Transactions of 6th Congress of International Soil Science Society. Moscow: Society of Soil Science, 17-21. [Cited Within:1]
[15] Lehmann J, Joseph S. 2009. Biochar for Environmental. London: London Press, 1-12. [Cited Within:1]
[16] Lehmann J. 2007. A hand ful of carbon. Nature, 447(7141): 143-144. [Cited Within:1]
[17] Li Z, Wu P T, Feng H, et al. 2009. Simulated experiment on effect of soil bulk density on soil infiltration capacity. Transactions of the CSAE, 25(6): 40-45. (in Chinese) [Cited Within:1]
[18] Liu C C, Li Y, Ren X, et al. 2011. Applicability of four infiltration models to infiltration characteristics of water repellent soils. Transactions of the CASE, 27(5): 62-67. (in Chinese) [Cited Within:1]
[19] Liu H J, Liu J H, Yu J, et al. 2012. Effects of soil amendment on soil physical and chemical properties in oat field. Advanced Materials Research, 610-613: 2937-2943. [Cited Within:1]
[20] Liu J L, Ma X Y, Zhang Z H. 2010. Applicability of explicit functions on cumulative infiltration of Green-Ampt model under different conditions. Journal Basic Science and Engineering, 18(1): 11-19. (in Chinese) [Cited Within:1]
[21] Mao L L, Lei T W, Bralts V F. 2011. An analytical approximation method for the linear source soil infiltrability measurement and its application. Journal of Hydrology, 411(3): 169-177. [Cited Within:1]
[22] Marris E. 2006. Putting the carbon back: black is the new green. Nature, 442(7103): 624-626. [Cited Within:1]
[23] Mezencev V J. 1948. Theory of formation of the surface runoff. Meteorologia. I Gidrologia, 3: 33-46. (in Russian) [Cited Within:1]
[24] Mishra S K, Tyagi J V, Singh V P. 2003. Comparison of infiltration models. Hydrological Processes, 17(13): 2629-2652. [Cited Within:2]
[25] Moore I D, Larson C L, Slack D C, et al. 1981. Modelling infiltration: a measurable parameter approach. Journal of Agricultural Engineering Research, 26(1): 21-32. [Cited Within:1]
[26] Parchami-Araghi F, Mirlatifi S M, Dashtaki S G, et al. 2013. Point estimation of soil water infiltration process using Artificial Neural Networks for some calcareous soils. Journal of Hydrology, 481: 35-47. [Cited Within:1]
[27] Parhi P K, Mishra S K, Singh R. 2007. A modification to Kostiakov and modified Kostiakov infiltration models. Water Resources Management, 21(11): 1973-1989. [Cited Within:1]
[28] Philip J R. 1957. The theory of infiltration: 1. The infiltration equation and its solution. Soil Science, 83(5): 345-358. [Cited Within:1]
[29] Qi R P, Zhang L, Yan Y H, et al. 2014. Effects of biochar addition into soils in semiarid land on water infiltration under the condition of the same bulk density. Chinese Journal of Applied Ecology, 25(8): 2281-2288. (in Chinese) [Cited Within:1]
[30] Rashidi M, Seyfi K. 2007. Field comparison of different infiltration models to determine the soil infiltration for border irrigation method. American-Eurasian Journal of Agricultural & Environmental Sciences, 2(6): 628-632. [Cited Within:1]
[31] Shukla M K, Lal R, Unkefer P. 2003. Experimental evaluation of infiltration models for different land use and soil management systems. Soil Science, 168(3): 178-191. [Cited Within:2]
[32] Sohi S, Lopez-Capel E, Krull E, et al. 2009. Biochar, climate change and soil: a review to guide future research. CSIRO Land and Water Science Report, 17-31. [Cited Within:1]
[33] US Department of Agriculture, Natural Resources and Conservation Service. 1974. National Engineering Hand book. Section 15. Border Irrigation. Washington, DC: National Technical Information Service. [Cited Within:1]
[34] Valiantzas J D. 2010. New linearized two-parameter infiltration equation for direct determination of conductivity and sorptivity. Journal of Hydrology, 384(1-2): 1-13. [Cited Within:1]
[35] Van de Genachte G, Mallants D, Ramos J, et al. 1996. Estimating infiltration parameters from basic soil properties. Hydrological Processes 10(5): 687-701. [Cited Within:1]
[36] Wang T T, Ma J B, Qu D, et al. 2017. Characteristics and mechanism of copper adsorption from aqueous solutions on biochar produced from sawdust and apple branch. Environmental Science, 38(5): 2161-2171. (in Chinese) [Cited Within:1]
[37] Yan Y H, Zheng J Y, Zhang X C, et al. 2013. Impact of biochar addition into typical soils on field capacity in Loess Plateau. Journal of Soil and Water Conservation, 27(4): 120-124. (in Chinese) [Cited Within:1]
[38] Zhao X N, Wu F Q. 2004. Developments and reviews of soil infiltration research. Journal of Northwest Forestry University, 19(1): 42-45. (in Chinese) [Cited Within:1]
[39] Zheng J Y, Stewart C E, Cotrufo M F. 2012. Biochar and nitrogen fertilizer alters soil nitrogen dynamics and greenhouse gas fluxes from two temperate soils. Journal of Environmental Quality, 41(5): 1361-1370. [Cited Within:1]