Mining operations can usually lead to environmental deteriorations. Underground mining activities could cause an extensive decrease in groundwater level and thus a dramatic variation in soil moisture content (SMC). In this study, the spatial and temporal variations of SMC from 2001 to 2015 at two spatial scales (i.e., the Shendong coal mining area and the Daliuta Coal Mine) were analyzed using an improved thermal inertia model with a long-term series of Landsat TM/OLI (TM=Thematic Mapper and OLI=Operational Land Imager) data. Our results show that at large spatial scale (the Shendong coal mining area), underground mining activities had insignificant negative impacts on SMC and that at small spatial scale (the Daliuta Coal Mine), underground mining activities had significant negative impacts on SMC. Trend analysis of SMC demonstrated that areas with decreasing trend of SMC were mainly distributed in the mined area, indicating that underground mining is a primary cause for the drying trend in the mining region in this arid environment.
Impact of mining activities on environments has been one of the research foci in ecology and environment sciences (e.g., Bell et al., 2000; Charou et al., 2010; Pandey et al., 2014). It was abundantly reported that mining activities have adverse impacts on environments (Bell et al., 2000; Tripathi et al., 2009). The most visible adverse impacts include land subsidence and ground fissures, but the long-lasting adverse impacts are land degradation-related (Bell et al., 2000; Wei et al., 2006; Li et al., 2009; Lei et al., 2010; Zang et al., 2010; Zhao et al., 2010). For examples, Townsend et al. (2009) demonstrated that mining activities can negatively affect the regional watershed hydrology; Pandey et al. (2014) found that mining activities could change plant community structure. Most relevant to this study is the work by Yang et al. (2016) showing that mining activities could inevitably change soil physical-chemical properties by reducing soil moisture content (SMC), soil cohesion and soil organic matter content. The work by Zang et al. (2010) further stressed that SMC suffered the worst effects from mining activities.
SMC, the link between precipitation and groundwater (Song et al., 2011), is the most significant factor limiting vegetation growth in arid regions (Zhuang and Zhao, 2008). It is also an essential element in processes that drive land surface water and energy fluxes (Ephrath et al., 1996; Zheng and Eltahir, 1998; Van Doninck et al., 2011; Chang et al., 2012; Maltese et al., 2013), which could affect ecosystem dynamics and biogeochemical cycles in the land-atmosphere system (Chen and Hu, 2004; Verstraeten et al., 2006). Accurate estimate of SMC at large spatial scales using the traditional SMC field measurements is diffi cult to achieve because the field measurements are labor-intensive and time-consuming (Minacapilli et al., 2009). By contrast, remote sensing (RS) techniques are the effective and economical ways to monitor SMC at large spatial scales (Maltese et al., 2010).
The thermal inertia method has been widely used for soil moisture retrieval from short-wave and long-wave remote-sensing data (Murray and Verhoef, 2007; Maltese et al., 2010). For example, Maltese et al. (2010) demonstrated that the thermal inertia approach allowed prediction of the spatial distribution of SMC with a satisfactory level of accuracy. Cai et al. (2007) developed a thermal inertia model for SMC estimates using the MODIS images and the model is suitable in situations where either the satellite overpass time coincides with the local maximum and minimum temperature time or not. One specific issue of this model is to obtain the soil temperature difference with high spatial resolution. Only few satellite sensors can provide the diurnal soil temperature difference, e.g., MODIS sensor and NOAA/AVHRR sensor (Lei et al., 2014). However, the deficiency of MODIS sensor and NOAA/AVHRR sensor is that both soil temperature difference and soil moisture retrieved from those images are at a relatively coarse spatial resolution (1 km). Furthermore, many studies have established numerous functional models between thermal inertia and SMC (e.g., Ma, 1997; Murray and Verhoef, 2007; Lu et al., 2009). Among which, the model proposed by Ma (1997) is a widely-used one because it only includes two simple variables, i.e., solid particle density and water content. By contrast, the other models often require a precise description of soil properties, such as soil thermal conductivity and porosity (Maltese et al., 2013).
Coal energy consumption is significant in China and underground mining is the major practice of China’ s coal mining (Ma, 2013). Underground mining activities were reported to have caused many changes in the lithosphere, hydrosphere, atmosphere, biosphere and land cover at large spatial scales (Chen and Hu, 2004) and to have resulted in dramatic soil moisture changes in mining-led subsiding areas (Kong et al., 2016). Shendong coal mining area, a major energy base in China (Ma et al., 2013), is a vulnerable ecological region with deep groundwater table (8-35 m before mining), high evaporation and low precipitation (Liu, 2013). The impacts of underground mining activities on SMC in the Shendong coal mining area have been widely investigated (He et al., 2007; Bian et al., 2009a; Zhao et al., 2010; Bi et al., 2014; Ma et al., 2014; Li et al., 2016; Tai et al., 2016). These previous studies mainly focused on the comparison of SMC between mined and unmined areas either based on the limited field tests or solely based on RS data or simply focused on the relationship between SMC and collapse fissures resulted from mining activities (Wei et al., 2006; He et al., 2007; Bian et al., 2009a; Zhao et al., 2010; Zang et al., 2012; Liu, 2013; Ma et al., 2013; Li et al., 2016). Nevertheless, knowledge about the impacts of underground mining activities on SMC from multi-temporal aspects and multi-scale perspectives is scare.
In this study, we expanded an improved thermal inertia model by introducing a sine model to improve the spatial resolution of SMC estimations. The spatial and temporal variations of SMC in the Shendong coal mining area were quantified and the impacts of underground mining activities on SMC were evaluated at two different spatial scales. The aims of this study were to: (1) address the spatial distributions of SMC at two spatial scales during the period of 2001-2015; and (2) determine the temporal variations of SMC at two spatial scales.
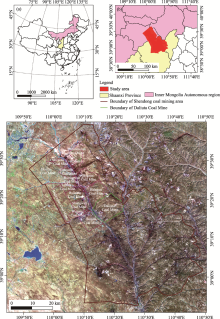
The study area is the Shendong coal mining area located at the border between Shaanxi Province and Inner Mongolia Autonomous Region, China (1000-1500 m a.s.l; Fig. 1). The total area is approximately 3.214× 103 km2. The western and southern parts are encompassed by the Hobq Desert and the Mu Us Sandy Land, respectively (Bian et al., 2009a). Average annual precipitation is 360 mm and average annual evaporation is approximately 2300 mm. It should be noted that about 70% of the annual total precipitation occurs in August and September. The primary soil type is sand and the area is geographically characterized by an aeolian landform with sparse vegetation (Lei et al., 2010, 2014).
Shendong coal mining area is affiliated to the Shendong Coal Company. There are a total of 15 coal mines distributed in the area (such as Bulianta Coal Mine, Daliuta Coal Mine, Huojitu Coal Mine, etc.), with the total production capacity of over 200× 106 t/a. It should be mentioned that Daliuta Coal Mine, located in Shenmu County of Shaanxi Province, is the first underground coal mine built in the Shendong coal mining area (in 1986). It has a production capacity of 20× 106 t/a with a designed service life of 119 years.
The Landsat series of satellites provides the longest continuous record of satellite-based observations (Qin et al., 2004; Sobrino et al., 2008; Chander et al., 2009; Jimé nez-Muñ oz et al., 2009). As such, Landsat is an invaluable resource for monitoring environmental changes (Fuller et al., 1994; Vogelman et al., 2001; Goward et al., 2006; Wulder et al., 2008). In this study, seven Landsat 5 (or 8) TM/OLI images spanning from 2001 to 2015 were selected (Table 1). By interpreting the satellite images, we classified land-cover types in the study area into four categories: bare land, bare rock/impervious surface, vegetated land, and water body. We then calculated the vegetation coverage of each land-cover type (Table 1).
| Table 1 Characteristics of the selected seven Landsat 5 (or 8) images |
To validate the estimations of SMC using TM/OLI images, we conducted in situ measurements of SMC in the Daliuta Coal Mine on 26 September, 2013. A portable WET-2 sensor (Delta-T Devices, UK) was used for measuring the volumetric SMC. The positions of the sampling sites were recorded with a GPS receiver.
The hourly air temperature data were obtained from the China Meteorological Forcing Dataset (http://westdc.westgis.ac.cn/data/) and the adjacent meteorological stations around the study area. It should be noted that the hourly air temperature data from 2013 to 2015 were collected from the Yulin Meteorological Station and the Dongsheng Meteorological Station, because China Meteorological Forcing Dataset did not extend beyond 2012. Since the time interval of hourly air temperature data from the China Meteorological Forcing Dataset was 3 hours, we used the cubic spline interpolation (Borak and Jasinski, 2009) to scale the time interval down from 3 hours to 1 hour. Yearly precipitation and air temperature data provided by the Shendong Coal Company were obtained from local observation in Ulan Moron Town.
All visible light wave bands of the Landsat data were firstly resampled to a resolution of 30 m. As the atmospheric scattering effects should be removed prior to analysis to extract land cover information efficiently from Landsat data, we used the method of FLAASH (Fast Line-of-sight Atmospheric Analysis of Hypercubes) atmospheric correction to correct the visible light wave bands. FLAASH contains the MODTRAN 4+ radiation transmission model that has a high precision (Yuan et al., 2009). The Mono-window algorithm (Qin et al., 2001) was used for land surface temperature inversion. The influence of the atmosphere was considered in the process of calculation, therefore, atmospheric correction was unnecessary for the thermal infrared bands (Qin et al., 2003). Geometric calibration of Landsat images was then performed for the bands on scene 2 to scene 10 using scene 1 as a benchmark to ensure that the overall error would be controlled within 0.5 pixels. Then, the vector boundary of the study area was overlaid on all images to mask the study area.
For the thermal inertia model, it is critical to obtain the soil temperature difference. Only a few satellite sensors can provide the diurnal soil temperature difference, such as the MODIS sensor and NOAA/AVHRR sensor (Verstraeten et al., 2006). However, these sensors have a moderate spatial resolution (1 km). The Landsat TM/OLI images have higher spatial resolution (30 m) than the MODIS and NOAA/AVHRR images, but they cannot provide the day-night soil temperature difference (Lei et al., 2014). To solve this problem, we developed an improved thermal inertia model by integrating the land surface temperature derived from the TM/OLI images and a simple sine model to obtain the soil temperature difference.
2.3.1 Thermal inertia model
The thermal inertia (TI) can be calculated using the thermal inertia model developed by Cai et al. (2007) that is based on the MODIS images. The solution of TI was used in the first-order approximation of the Fourier series. It should be noted that following the real thermal inertia model of Xue and Cracknell (1995a), the thermal inertia model of Cai et al. (2007) was modified to be suitable in situations where either the satellite overpass time coincides with the local maximum and minimum temperature time or not.
The thermal inertia (TI) was calculated as follows (Cai et al., 2007):
$TI=\frac{(1-A){{S}_{0}}{{C}_{t}}{{A}_{1}}[\cos (\omega {{t}_{2}}-{{\delta }_{1}})-\cos (\omega {{t}_{1}}-{{\delta }_{1}})]}{\Delta T\sqrt{\omega }\sqrt{1+\frac{1}{b}+\frac{1}{{{b}^{2}}}}}, $ (1)
$b=\frac{\tan (\omega {{t}_{\max }})}{1-\tan (\omega {{t}_{\max }})}, $ (2)
${{\delta }_{1}}=\frac{b}{1+b}, $ (3)
where, A is the surface albedo; S0, the solar constant (S0=1367 W/m2); Ct, the atmospheric transmittance in the visible spectrum, typically equal to 0.75 (Xue and Cracknell, 1995b); A1, the coefficient of the Fourier series, which can be derived from solar declination and local latitude; ω (rad/s), the angular velocity of Earth’ s rotation; t1 and t2(s), the time of the MODIS satellite overpassing at day and night, respectively; δ 1, the phase difference in the first-order approximation of the Fourier series, which can be expressed as a function of b (Eq. 3); ∆ T(K), the land surface temperature difference during time t1 and t2; b, a process variable, which can be calculated from Equation 2; and tmax(s), the time of maximum temperature during the day.
2.3.2 Surface albedo
Before the determination of surface albedo, spectral reflectance in short wave radiation should be obtained (Cai et al., 2007). For TM/OLI images, the spectral reflectance in each band can be acquired using the FLAASH model. The broadband surface albedo (A) is the weighting function for converting spectral reflectance and can be calculated from Equation 4 (Liang, 2001):
$A=0.356{{\rho }_{ch.1}}+0.130{{\rho }_{ch.3}}+0.373{{\rho }_{ch.4}}+0.085{{\rho }_{ch.5}}+0.072{{\rho }_{ch.7}}-0.0018, $ (4)
For TM images, ρ ch.1, ρ ch.3, ρ ch.4, ρ ch.5 and ρ ch.7 refer to the surface reflectance from bands 1, 3, 4, 5 and 7, respectively; and for OLI images, ρ ch.1, ρ ch.3, ρ ch.4, ρ ch.5 and ρ ch.7 refer to the surface reflectance from bands 2, 4, 5, 6 and 8, respectively.
2.3.3 Diurnal land surface temperature difference (∆ T)
In the study of Cai et al. (2007), ∆ T is the diurnal land surface temperature difference during the MODIS satellite overpass time t1 and t2 at day and night. However, TM/OLI images were used in this study, we thus introduced a new method to obtain ∆ T and tmax.
A simple sine model that describes the diurnal land surface temperature difference was established in this study. It has been widely reported that the diurnal cycles of land surface temperature and air temperature can be approximately described as sine curves (Xue and Cracknell, 1995a; Campbell and Norman, 1998; Cai, 2006; Stisen et al., 2007; Jiang et al., 2010; Ma et al., 2013). Therefore, we assumed that both diurnal air temperature and land surface temperature are the sine functions of time t.
${{T}_{\text{air}}}={{M}_{1}}\sin ({{a}_{1}}t+{{b}_{1}})+{{c}_{1}}, $ (5)
${{T}_{ls}}={{M}_{2}}\sin ({{a}_{2}}t+{{b}_{2}})+{{c}_{2}}, $ (6)
where, Tair (K) is the air temperature at time t; Tls(K) is the land surface temperature at time t; M1 and M2 (K) are the amplitude of the sinusoidal components; a1, a2, b1 and b2 are the parameters to calculate the phase; and c1 and c2 (K) are the offsets.
According to above assumption, we obtained ∆ Tand tmaxthrough the following three steps.
First, the air temperature sine model (Eq. 5) was fitted by inputting air temperature data obtained from the local meteorological stations and the China Meteorological Forcing Dataset, and then the parameters a1, b1, andc1were obtained (Fig. 2).
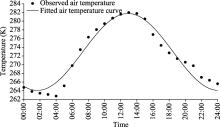 | Fig. 2 Observed hourly data of air temperature and fi tted air temperature curve after sine function (11 November, 2015) |
Second, the land surface temperature sine model (Eq. 6) was derived from the fitted air temperature sine model. The prerequisite for estimating diurnal land surface temperature is that the land surface temperature and air temperature are not out of phase. The prerequisite is fulfilled from the morning to the midday. It was reported that the phase shift only occurs approximately 2.5 h after solar noon (Rosenberg et al., 1974). In addition, the diurnal minimum air temperature and land surface temperature are rather close (Stisen et al., 2007), implying that the offset of the air temperature sine model (Eq. 5) can be approximately substituted for the land surface temperature. Therefore, the parameters a2, b2, and c2 are approximately and respectively equal to the parameters a1, b1, and c1, which have been restricted to the time period of 00:00-14:30 (Beijing time). Thus, Equation 6 can be rewritten as Equation 7:
${{T}_{ls}}={{M}_{2}}\sin ({{a}_{1}}t+{{b}_{1}})+{{c}_{1}}.$ (7)
Since the Tls at the time of TM/OLI image acquisition can be obtained from the land surface temperature inversion, the amplitude (M2) of land surface temperature sine model was calculated from Equation 7.
Third, the ∆ Tand tmax were obtained from Equation 7. The value of tmax can be directly obtained from Equation 7. When the t1 and t2 are known, the value of ∆ Tcan be calculated from Equation 7 because ∆ T is equivalent to Tls at t1 minus Tls att2. It should be noted again that the model developed by Cai et al. (2007) is suitable in situations where either the satellite overpass time coincides with the local maximum and minimum temperature time or not. Thus, we consistently set t1 at 11:00 (the general overpass time of Landsat) and t2 at 02:00 (the general time of minimum land surface temperature) for all the calculation data to reduce errors.
2.4.1 SMC estimation
The relationship between thermal inertia and SMC in the M model is as follows (Ma, 1997):
$TI={{\left. {{\left\{ 2.1{{d}_{s}} \right.}^{(1.2-0.02{{d}_{P}}{{\omega }_{w, s}})}}\times \exp [-0.007{{({{d}_{P}}{{\omega }_{w, s}}-20)}^{2}}]+{{d}_{s}}^{(0.8+0.02{{d}_{P}}{{\omega }_{w, s}})} \right\}}^{\frac{1}{2}}}\times (0.2+\frac{{{d}_{P}}{{\omega }_{w, s}}}{100}){{d}_{s}}\times \sqrt{\frac{1}{1000}}, $ (8)
where, ds (g/cm3) is the soil particle density; dp is the relative soil particle density, which is equal to the average soil density divided by the water density, i.e., it is a dimensionless physical constant (2.65); and ω w, s (%) is the weight percentage of SMC. Then, a lookup table can be established, which is composed of thermal inertia, soil particle density and SMC. Finally, the SMC can be estimated from thermal inertia by means of the lookup table. It should be particularly noted that the improved thermal inertia model is only suitable for bare soils or sparsely vegetated areas.
2.4.2 SMC validation
SMC was in suit measured by a portable WET-2 sensor at the No. 52303 Mining Face in the Daliuta Coal Mine. To minimize the impacts of land topography and geomorphology, we selected ten sampling sites with uniform slope (about 0.30-0.35) and with similar soil types and vegetation coverages. To avoid the possible disturbances of mining subsidence, we selected 5 sampling sites in the subsidence basin (No. 1-5 sampling sites in Table 2) and 5 sampling sites in the un-subsidence area (No. 6-10 sampling sites in Table 2). The distance between two adjacent sampling locations was about 30 m. SMC was measured at 5-cm depth with three replicates in each sampling site.
| Table 2 Comparisons between measured soil moisture content (SMC) data and estimated SMC data from Landsat TM/OLI images |
We first established the statistical relationship between the modelled data using the improved thermal inertia model and the in situ SMC data. Again, it should be noted that the in situ SMC measurements were conducted at approximately the same time as the image was taken (i.e., on 29 September, 2013) for validation, i.e., on 26 September, 2013. The estimated data from the RS-derived thermal inertia were gravimetric SMC values, which are different from the in situvolumetric SMC values. Thus, the estimated SMC data should be inverted into the volumetric values by multiplication of soil particle density (see Table 2).
Regression analysis was used for the validation (data not shown). Generally speaking, the estimated SMC agreed well with thein situ SMC (with R2 value of 0.9398), indicating that the improved thermal inertia model performed rather well. Furthermore, the average difference betweenin situ SMC and estimated SMC from the TM/OLI images was 2.52% (Table 2), being lower than the result from the MODIS images of Cai et al. (2007).
In this study, all statistical analyses were performed using Microsoft Excel 2010 (Microsoft Inc., Redmond, Washington, USA). The simple linear regression method and the Pearson correlation coefficient were both used to describe the relationship between SMC and influencing factors (e.g., precipitation and air temperature). Difference was considered significant at P< 0.05 level. Furthermore, all figures were plotted using Origin 9.1 software.
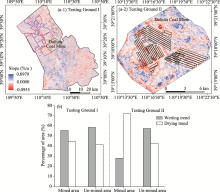
In this study, we chose two different spatial scales to delineate the spatial and temporal variations of SMC and to assess the impacts of underground mining activities on SMC. In addition, the values of SMC in the mined and un-mined areas at each spatial scale were compared. The first spatial scale was the Shendong coal mining area testing ground (hereinafter called Testing Ground I) and the second spatial scale was the Daliuta Coal Mine testing ground (hereinafter called Testing Ground II). Spatial illustration of the two testing grounds as well as the mined area and un-mined area at each testing ground are shown in Figure 3. The mined area at Testing Ground I (909.12 km2) was within the concentrated mining area (i.e., northwestern part) of the Shendong coal mining area, while the un-mined area (2304.88 km2) was mainly distributed in the southern and southeastern parts of the Shendong coal mining area.
3.1.1 Spatial variations of SMC at Testing Ground I
To detect whether underground mining is the dominant factor impacting the SMC at Testing Ground I, we compared the difference of mean SMC between mined area and un-mined area from 2001 to 2015. As shown in Table 3, mean SMC values in the mined area were slightly lower than those in the un-mined area during the period from 2001 to 2015.
| Table 3 Comparison of mean SMC between mined area and un-mined area at Testing Ground I |
3.1.2 Spatial variations of SMC at Testing Ground II
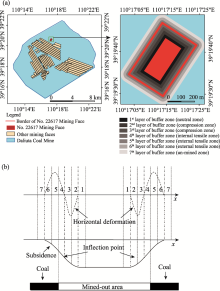
In this study, we selected the No. 22617 Mining Face in the Daliuta Coal Mine to delineate the spatial variations of SMC at Testing Ground II. Furthermore, spatial distributions of SMC in the pre-mining period and post-mining period were analyzed. Because No. 22617 Mining Face was active in 2011, SMC values in 2009 were selected as the pre-mining data and SMC values in 2014 were selected as the post-mining data. Consequently, we calculated the mining disturbance zones of No. 22617 Mining Face based on the theory of mining subsidence (Guo and Chai, 2013). As shown in Figure 4, the mining disturbance zones at No. 22617 Mining Face consisted of the neutral zone, compression zone, internal tensile zone, and external tensile zone. To analyze the effect of these mining disturbance zones, we set the mining face as the boundary using ArcGIS software. Finally, 3 buffer zones were established outward and 4 buffer zones were established inward at an interval of 20 m. Each buffer zone approximately corresponded to a specific mining disturbance zone (Fig. 4).
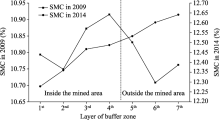
Average SMC values in each layer of buffer zone at No. 22617 Mining Face in the Daliuta Coal Mine in the pre-mining period (taken 2009 as the representative) and post-mining period (taken 2014 as the representative) are shown in Figure 5. Average SMC values showed an irregular trend in the pre-mining period and an increasing trend in the post-mining period along the layers of buffer zones. Due to the underground mining activities, the SMC clearly decreased from the un-mined zone (i.e., the 7th layer of buffer zone) to the neutral zone (i.e., the 1st layer of buffer zone). These results indicated that SMC was significantly impacted by underground mining activities, not only inside the mined area but also outside the mined area (near the boundary of the mined area in the external tensile zone).
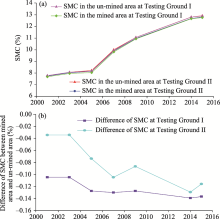
Inter-annual variations of area-averaged SMC in the mined area and un-mined area at two testing grounds (Testing Ground I and Testing Ground II) from 2001 to 2015 are shown in Figure 6a. Values of area-averaged SMC at Testing Ground I and Testing Ground II were nearly identical. During the entire study period (2001-2015), a pronounced increasing trend of area-averaged SMC was observed. The difference of area-averaged SMC between mined area and un-mined area at the two testing grounds could be used to examine the impacts of underground mining activities on SMC. It can be seen from Figure 6b that with increased underground mining activities, the absolute value of the difference in area-averaged SMC between mined area and un-mined area gradually increased during the entire period. The results revealed that underground mining activities have significant impacts on SMC, especially at a mining face (see section 3.1.2).
To estimate long-term trend variation of SMC, we calculated the linear trend for every pixel of SMC using the linear regression model (Wei, 2007). The simple linear regression model was built with the parameters of time and SMC. The linear trend of SMC from 2001 to 2015 was calculated using the generalized linear equation (Wei, 2007):
$SMC=slope\times year+b, $ (9)
$Slope=\frac{\sum\nolimits_{i=1}^{n}{SM{{C}_{i}}{{T}_{i}}}-\left( \sum\nolimits_{i=1}^{n}{SM{{C}_{i}}} \right)\times \frac{\left( \sum\nolimits_{i=1}^{n}{{{T}_{i}}} \right)}{n}}{\sum\nolimits_{i=1}^{n}{T_{i}^{2}}-\frac{{{\left( \sum\nolimits_{i=1}^{n}{{{T}_{i}}} \right)}^{2}}}{n}}, $ (10)
where, slope (%/a) is the tendency value of SMC during the period of 2001-2015; b (%) is the intercept; n is the number of years (equal to 8 here); Ti is the ith year beginning from 2001; and SMCi (%) is the soil moisture content in the ith year. The value of slope represents the trend of SMC during the period of 2001-2015. The positive slope values represent increases of SMC (wetting trend) while the negative slope values represent decreases of SMC (drying trend). The spatial patterns of trends in SMC during the period of 2001-2015 are shown in Figures 7a-1 and a-2. There was a significant spatial heterogeneity of SMC throughout the study area during the period of 2001-2015. Overall, areas with signifi cant decreasing trend of SMC were distributed primarily in the surrounding region of the water body and also in the grasslands of the southeastern and northeastern regions.
To further detect the impacts of underground mining activities on SMC during the period of 2001-2015, we calculated the proportional areas of positive and negative slope pixels (Fig. 7b). For Testing Ground I, the wetting trend was dominant both in the mined area and un-mined area, and the percentage of area with wetting trend was higher in the un-mined area than in the mined area. However, the percentage of area with drying trend was 3.09% higher in the mined area than in the un-mined area. For Testing Ground II, the percentage of area with drying trend in the mined area was approximately 1.69-fold higher than that in the un-mined area.
Mining operations usually exert negative impacts on environments. Specially, in a mining area within arid environments, mining activities affect the growth of plants by changing the amount of available water in soils (Bian et al., 2009a). In this study, the SMC values in the mined area were always lower than those in the un-mined area during the period of 2001-2015 in the Shendong coal mining area, implying that underground mining activities did exert negative impacts on SMC (Bian et al., 2009b; Lei, 2009; Zhao et al., 2010; Qie et al., 2015). Furthermore, the impacts of underground mining activities on SMC were more evident at small spatial scale than at large spatial scale. For the Shendong coal mining area, underground mining activities had insignificant negative impacts on SMC. For the Daliuta Coal Mine, the impacts of underground mining activities on SMC are significantly negative and exhibited regularities in spatial distribution. At small spatial scale (e.g., at the No. 22617 Mining Face), we found that the impacts of underground mining activities on SMC are significantly negative and the SMC gradually decreased from the external tensile zone to the neutral zone. It was previously reported that underground mining activities resulted in a dramatic decrease of groundwater level in the Daliuta Coal Mine area (Lei et al., 2010).
Trend analysis of SMC during the period of 2001-2015 showed that at two spatial scales (the Shendong coal mining area and the Daliuta Coal Mine), area with drying trend (SMC decreasing trend) was higher in the mined area than in the un-mined area, indicating that underground mining is a primary cause for the drying trend in the mining region within arid environments (Bian et al., 2009b; Lei, 2009).
To assess the impacts of other factors on the variations of SMC at temporal scales, we compared the inter-annual variations of SMC (averaged SMC in the Shendong coal mining area) and climate factors (precipitation and air temperature) from 2001 to 2015 (Fig. 8). The similar increasing trends of SMC and precipitation during the period of 2001-2015 may suggest that the SMC increasing trend was a result of the precipitation increasing trend. But, admittedly, we are deeply bothered by that fact that SMC increasing trend is also accompanied with air temperature increasing trend and it is certainly anti-intuitive to explain the increasing SMC trend using the increasing air temperature trend. It implies that the climatic attribution of the SMC increasing trend should be further examined.
In this study, the spatial and temporal variations of SMC in the Shendong coal mining area and also in the Daliuta Coal Mine were determined using the improved thermal inertia model with a long-term series of TM/OLI data. We found that the improved thermal inertia method is useful for estimating SMC with high spatial resolution in bare soils or sparse vegetation areas in arid regions. Underground mining activities impact on SMC mainly at spatial scales. Taking into consideration of the detrimental impacts of underground mine subsidence on SMC, measures such as filling the cracks, are recommended to alleviate this adverse impact. As the impacts of underground mining activities on the spatial and temporal variations of SMC are a complex process, more detailed studies on the relationships between SMC and underground mining activities are needed.
This study was supported by the National Natural Science Foundation of China (U1361214) and the National Key Research and Development Program of China (2016YFC0501107).
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
|
| [47] |
|
| [48] |
|
| [49] |
|
| [50] |
|
| [51] |
|
| [52] |
|
| [53] |
|
| [54] |
|
| [55] |
|
| [56] |
|
| [57] |
|
| [58] |
|
| [59] |
|
| [60] |
|
| [61] |
|
| [62] |
|