Velocity is a key parameter characterizing the movement of saltating particles. High-speed photography is an efficient method to record the velocity. But, manually determining the relevant information from these photographs is quite laborious. However, particle tracking velocimetry (PTV) can be used to measure the instantaneous velocity in fluids using tracer particles. The tracer particles have three basic features in fluids: similar movement patterns within a small region, a uniform particle distribution, and high particle density. Unfortunately, the saltation of sand particles in air is a stochastic process, and PTV has not yet been able to accurately determine the velocity field in a cloud of blowing sand. The aim of the present study was to develop an improved PTV technique to measure the downwind (horizontal) and vertical velocities of saltating sand. To demonstrate the feasibility of this new technique, we used it to investigate two-dimensional saltation of particles above a loose sand surface in a wind tunnel. We analyzed the properties of the saltating particles, including the probability distribution of particle velocity, variations in the mean velocity as a function of height, and particle turbulence. By automating much of the analysis, the improved PTV method can satisfy the requirement for a large sample size and can measure the velocity field of blowing sand more accurately than previously-used techniques. The results shed new light on the complicated mechanisms involved in sand saltation.
Any aeolian movement starts with the movement of individual particles. Three main modes of aeolian movement have been identified (Bagnold, 1941), namely suspension, saltation, and creep. Of these, saltation attracts the most interest from researchers. This is because: (1) saltation is the most important mode, accounting for 50% to 75% of the total aeolian transport (Bagnold, 1941; Chepil, 1945); (2) saltation is the key link in transferring momentum between the air and the underlying bed, and between particles in air (Dong et al., 2006, 2007); and (3) saltation is the most easily studied process, both theoretically and experimentally. However, progress in describing the movement of saltating particles has been slow. The difficulty of obtaining a sufficient sample size and sufficiently accurate data has greatly impeded progress in understanding this phenomenon.
Research into particle movement during saltation can be conducted by using both theoretical and experimental methods. Theoretical methods are primarily based on known physical processes (Anderson and Haff, 1988, 1991; Zou et al., 1992; Hopwood and Scott, 1997). For example, the velocity of a saltating grain is usually calculated using equations that describe particle motion based on known or assumed initial conditions, such as the ejection velocity and liftoff angle of a particle. However, the factors influencing grain movement through the air are multiple and mainly include downwind acceleration by the wind, mid-air inter-particle collisions, initial and subsequent impacts on the bed, the Magnus force associated with particle rotation, and the Saffman force resulted from air shear (Saffman, 1965; White and Schulz, 1977; Sø rensen and McEwan, 1996). These factors are usually difficult to be fully considered in theoretical models (Zou et al., 2001; Zheng et al., 2004) and consequently, an accurate theoretical model of saltation processes has yet to be developed.
Experimental investigations of particle velocity depend on the measurement techniques. Several techniques have been applied to measure the velocity of blowing particles, including high-speed photography, particle-dynamics analyzers (PDA), and particle image velocimetry (PIV) (Hunt and Nalpanis, 1985; White, 1985; Rasmussen and Mikkelsen, 1991; White and Mounla, 1991; Willetts et al., 1991; Williams et al., 1994; Zou et al., 2001; Dong et al., 2002a, b, 2004; Yang et al., 2007). Each technique is based on one or more unique principles, and has its advantages and disadvantages.
The saltation of sand particles in air has been shown to be a stochastic process and it is thus essential to do simultaneous statistical analysis of data from different heights for studying the mechanisms responsible for wind-saltation interactions. PDA, which employs a phase Doppler technique, can measure a large number of samples that pass a point within a few seconds according to the light scattered by the particles. However, the measurements are not strictly simultaneous because PDA is a point measurement technique although the traverse system was precise and fast (Dong et al., 2002a, b, 2004).
In contrast, PIV is a whole-flow-field technique that provides instantaneous velocity vector measurements in a cross-section of a flow. In PIV, images recorded by a camera during two closely spaced light pulses can be divided into small subsections that are called “ interrogation areas” . The interrogation areas from each pair of image frames can be cross-correlated with each other, pixel by pixel, using a binary image cross-correlation method that employs a fast Fourier transformation to obtain the particle’ s velocity. The cross-correlation produces a signal peak that identifies the displacement of a given particle between the two images. A third-order-polynomial sub-pixel interpolation method is used to accurately measure the particle’ s displacement, and thus, its velocity. A velocity vector map is obtained for the whole target area by repeating the cross-correlation for a given interrogation area for each pair of image frames captured by the camera. Because PIV deals with the intensity distribution within the interrogation window, it is mainly applied to the heavily seed flow conditions. In addition, it produces an averaged velocity at a representative point within the interrogation window, which in turn limits the spatial resolution unless super-resolution PIV is possible (Keane et al., 1995). For the flow of saltating particles, there is high heterogeneity in the particle velocities due to the existence of two distinct grain populations: ascending and descending grains. As a result of this complexity, the dynamic range of the standard PIV method is often saturated, and severe limitations occur in the ability to measure certain flow parameters.
Particle tracking velocimetry (PTV), as an alternative technique, can overcome these limitations. In contrast with PIV, PTV evaluates particle displacement by tracking individual particle images in consecutive image frames, thereby eliminating the need for spatial correlation analysis. This technique measures one vector for each particle rather than for each window, as would be the case in PIV (Stitou and Riethmuller, 2001; Qu et al., 2004). The approach is based on two major sub-processes, namely particle identification and particle tracking. Algorithm development to permit tracking of particles, which is essential for the success of PTV, has been the focus of PTV research, and the solutions can be divided into two categories. The first is based on minimizing the variation of the lengths and angles of the particle tracks between consecutive image frames, as in the three-frame or four-frame PTV algorithms (Hassan and Canaan, 1991; Kobayashi et al., 1991; Maas et al., 1993). The second relies on a statistical calculation of the probabilities of particle matches and an iterative updating process to determine the most probable particle path between frames, as in the two-frame PTV algorithm (Baek and Lee, 1996). The three- or four-frame algorithm is useful in scarcely seeded flows, whereas the two-frame algorithm is more suitable for the conditions where seeding density is high, particle distribution is uniform, and the movement is similar in the adjacent areas.
The flow of saltating particles in air is very complex, as the distribution of particles is non-uniform and the heterogeneity of the particle velocities in neighboring areas is high. Thus, none of these algorithms are well suited for measuring saltating particles in air. Although most observations of blowing sand since the 1970s have been obtained in a wind tunnel using high-speed photography to record consecutive images of the particles (White and Schulz, 1977; Willetts and Rice, 1985, 1986; Rice et al., 1995, 1996; Zou et al., 2001; Zhang et al., 2007; 2008; Tong and Huang, 2012; Fu et al., 2013), accurate description of individual particle trajectories has relied on laborious manual interpretation methods that make it difficult to obtain a statistically significant sample size.
In the present study, we developed a novel two-frame PTV algorithm based on the concept of maximizing the match efficiency. This approach overcomes the disadvantages of the conventional three- or four-frame PTV method. In addition, it is more suitable than the conventional two-frame PTV method (Baek and Lee, 1996) for analyzing trajectories in complex high-density flows. We evaluated the performance of this method by investigating the two-dimensional saltation characteristics of particles over a loose sand surface in a wind tunnel. We statistically analyzed the transport properties of the saltating particles, such as the probability distribution for particle velocity, variations of the mean velocity as a function of height, and particle turbulence. The results show that the improved PTV technique can satisfy the requirement for a large sample size and can measure the velocity field of a blowing sand cloud more accurately than the previously-used technique. The results will shed new light on the complicated motions that occur during saltation.
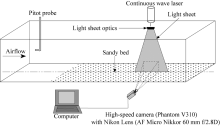
The experiment was performed in a blowing-sand wind tunnel at the Key Laboratory of Desert and Desertification of the Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences (Fig. 1). The blow-type, non-circulating wind tunnel has a total length of 10.5 m, with a 4-m-long test section. The cross-sectional area of the test section is 0.4 m high and 0.4 m wide. The free-stream wind velocity in the wind tunnel can be varied from 1 to 35 m/s. To ensure that the test airflow is aerodynamically rough, a roughness array at the front of the working section enhances boundary layer development in the working section, and the thickness of the boundary layer in the test section is more than 120 mm.
The main goals of our experiments were to test the reliability of the improved PTV algorithm and to demonstrate its usefulness in researching the transport properties within a cloud of blowing sand. The suitability of a wind tunnel for studying such phenomena depends on its Froude number, which is calculated as follows:
Fr = U2/(g× H), (1)
where Fr is the Froude number (dimensionless); U is the free-stream wind velocity (m/s); H is the height of the working section of the wind tunnel (m); and g is the acceleration due to gravity (9.8 m/s2).
Owen and Gillette (1985) reported that Fr> 20 would create pressure disturbances and adversely affect saltation because it would cause some particles to hit the wind tunnel’ s ceiling. To reduce the occurrence of such phenomena, we maintained the wind speed at less than 9 m/s in this study. Free-stream wind velocities were measured using a Pitot-static probe at the start of the working section. Details of the velocity profile measurement are described by Luo et al. (2012).
The bottom surface of the working section was covered by dry, loose, well-rounded spherical artificial quartz sand gains with a mean diameter of 150 μ m and a density of 2.65× 103 kg/m3. The 10-mm-thick sand bed was held in place by two bars that were placed perpendicular to the wind direction, and was then carefully smoothed by applying a small uniform pressure. It took 30 to 60 s for the wind tunnel to reach the required equilibrium status of free-stream wind velocity.
We used a Phantom V310 high-speed digital camera (with 16 GB of RAM; Vision Research Company, http://www.visionresearch.com) to record the saltation trajectories within a vertical plane defined by the light sheet produced using an orthogonal 532-nm continuous-wave laser. During our measurements, we established a free-stream wind velocity of 6.5 m/s, which was equivalent to a friction velocity of 0.27 m/s. The frame rate, spatial resolution, and exposure time were adjusted to 5000 fps, 800× 600 pixels, and 1/5000 s, respectively. The image acquisition section was located 2 m downwind from the leading edge of the working section and the middle rear of the sand bed. Using a lens with a short focal length can provide a lower image amplification factor, corresponding to clearer images of the particles. For a given lens, the lowest image amplification factor can be obtained when the image distance equals the closest possible focusing distance. Accordingly, we chose a 60 mm AF Micro Nikkor f/2.8D lens (Nikon, Tokyo, Japan), and positioned the camera at the side wall of the wind tunnel. Adjusting the shooting distance makes the objectives on closest focus plane (about 0.22 m). During each 5.6-s experiment, we captured 28, 000 frames and transferred them to a computer’ s hard disk. We then converted each image to gray levels ranging from 0 to 255 (according to the color difference between the black background and the saltating particles). The view window of the camera was set to acquire a target area of about 60 mm wide× 45 mm high; this required an amplification factor of 0.075 to convert the pixels into millimeters.
Image processing involved two main steps: particle recognition and particle matching. Most high-speed photography experiments use a laser light sheet to illuminate the instantaneous flow field for the light-scattering saltating particles. In the PTV method, the centroid of each particle must be determined in each image frame. Given the discrete points for a particle in two sequential images, the next step is to match the particle’ s position in the first image with its corresponding position in the second image. Based on the elapsed time between images and the change in the position of the particle’ s centroid, we can determine its speed and trajectory (i.e., its vector).
Even though the particle images were taken with great care, particles close to the immobile floor of the wind tunnel usually had a low contrast with the background due to light reflection from the bed, making the particles difficult to distinguish from the bed. This problem can be solved by recognizing that pixels representing the bed and the background do not change between images, so any change that is detected will represent the movement of saltating particles. This change can be calculated by subtracting pairs of images to detect changes, using the following equation:
${{J}_{i}}(x, y)=\left\{ \begin{align} & 0 {{I}_{i+1}}(x, y)-{{I}_{i}}(x, y)\le \Phi \\ & {{I}_{i+1}}(x, y) {{I}_{i+1}}(x, y)-{{I}_{i}}(x, y)> \Phi \\ \end{align} \right., $ (2)
whereIi(x, y) and Ii+1(x, y) represent the grayscale values of the pixel at (x, y) in images I and i+1, respectively. Φ is the optimal segmentation threshold for an image, which should be neither too high nor too low. A too-high Φ value will cause the loss of some data close to the bed, whereas a too-low Φ will provide poor segmentation results. After several tests, we found that the most appropriate Φ values were slightly higher than the absolute average value of the nonzero gray level differences between consecutive images in the region close to the bed.
This preprocessing procedure greatly improved the contrast between the target (i.e., the particle) and its background. The next step was to observe the saltating particles more clearly in air and near the sand surface:
${{Q}_{i}}(x, y)=\left\{ \begin{align} & 0 {{J}_{i}}(x, y)\le \lambda \delta , \text{ background image} \\ & 1 {{J}_{i}}(x, y)> \lambda \delta , \text{ particle image} \\ \end{align} \right., $ (3)
where Qi(x, y) represents binary values in which the gray values of the entire field of the particle images, namely the Ji(x, y) values produced using Equation 1, are replaced by 1 or 0 to represent the target particles and the background, respectively. Δ represents the grayscale segmentation value that distinguishes the targets from the background by applying the dynamical threshold-binarization method (Ohmi and Li, 2000) to produce high-contrast images. The accommodation coefficient λ is used to optimize the ability to recognize the particles.
After this analysis, most of the individual particles are detected accurately. To determine the location of each particle, we determined its pixel coordinates. Then, we calculated the average value of a particle’ s pixel coordinates and used it to represent the centroid of every particle. Finally, we determined the centroids of the particle in consecutive images.
Each particle’ s centroid in the processed images can be enlarged to represent a regular disc with a characteristic particle diameter d by means of an image dilation technique that uses a “ disk dilation parameter” (Gonzalez et al., 2009). Each overlapped image of the target in a superposition of two consecutive dilated particle centroids was then labeled. According to the location of each particle’ s centroid obtained from the image recognition procedure, the centroids of particles in each overlapped target can be determined.
There are three types of possibilities in the overlapped images (Fig. 2). First, more than two particle centroids are contained in the overlapped images. Second, only two particle centroids appear in the overlapped image. Third, the image contains only one particle centroid in each of the two consecutive images. The third type was defined as an effective match. Consequently, selecting an appropriate value of the dilation parameter was an important step in effectively matching particles.
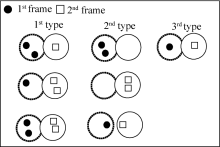 | Fig. 2 Types of match between consecutive particle images. The two circles show the overlapped particle images in the first (dotted lines) and second (solid lines) frames. |
In general, the density of saltating particles decreases and the mean particle velocity increases with increasing height. To improve the efficiency of our approach and decrease matching errors, we calculated different optimal image dilation coefficients at different heights. The maximum possible image dilation coefficient (n) can be determined by:
$n=\frac{{{v}_{_{\max }}}}{\omega }=\frac{U}{\omega }=\frac{U\Delta t}{\sigma }, $ (4)
where vmax is the maximum particle velocity (m/s); ω is the measurement precision (m/s); σ is the image amplification factor for converting the pixels into millimeters (mm/pixel); and Δ t is the time interval between two consecutive images (s).
The match efficiency for dilation coefficient κ between two consecutive dilation images ( 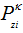
$P_{zi}^{k}=\frac{{{N}_{zk}}}{{{N}_{k}}(z)}\text{ }(k=1, 2, 3, ..., n), $ (5)
where Nκ (z) is the number of connected regions in the overlapped image of two consecutive images of the dilated particles and their centroids for dilation coefficient κ at height z; Nzκ is the number of matched targets at height z for dilation coefficient κ ; and n is the maximum possible value of the dilation coefficient.
Based on these definitions, we calculated the match efficiencies at different heights with different dilation coefficients. The optimal dilation coefficient corresponded to the κ value with the maximum match efficiency for a given height. Finally, we computed the velocity vectors of effectively matched particles based on their centroid locations using the following formula:
$\nu_{x}=(x_{i+1}-x_{i})/\Delta t; \ \ \nu_{y}=(y_{i+1}-y_{i})/\Delta t $ (6)
where vx and vy are the particle velocities in the horizontal and vertical directions (m/s), respectively; xi and xi+1 are the positions of the saltating sand grain along the horizontal axis in frames i and i+1 (m), respectively. Similarly, yi and yi+1 are the positions of the saltating sand grain along the vertical axis in frames i and i+1 (m), respectively.
At this point in the analysis, each pair of consecutive images has been completely processed. After analyzing each particle in the frames, the velocity distribution and the mean velocity at different heights can be obtained. Because all of the calculations can be performed automatically, without requiring manual calculations, this technique can be used to generate the large sample size required for accurate analysis of the saltation cloud.
As described in the improved new PTV method, it should be possible to use this method when there is a small time interval between consecutive images. However, small perturbations in the obtained centroid of the particle may lead to large errors in the computed velocity and acceleration. Thus, it is necessary to evaluate the accuracy of this method-produced result.
To quantify the accuracy, we defined the relative error of the results obtained by using the PTV method based on the measurement precision. In this context, the measurement precision represents the true velocity when a particle moved one pixel in a horizontal or vertical direction during the interval between two consecutive images. The relative error (E) is calculated as follows:
$E=\frac{||\nu_{true}|-|\nu_{mea}||}{|\nu_{true}|}\times 100%$ (7)
where vtrue and vmea represent the true velocity and the measured velocity (m/s), respectively. |vtrue|∈ [|vmea|, |vmea|+ω ].
According to Equation 6, the range of relative error values is E∈ [0, σ /(|vmea|Δ t)× 100%]. In addition, |vmea|=0 when |vtrue|< ω . In the present analysis, we assumed that |vtrue|≅ω /2. Consequently, the estimated value of the relative error can be expressed as follows:
$ \overline{E}= \left\{ \begin{aligned} \frac{\sigma}{2\Delta t|{v_{mea}}|}\times 100\%\ \ \ \ |{v_{mea}}|> 0 \\ 100\%\ \ \ \ |{v_{mea}}|> 0 \\ \end{aligned} \right. $ (8)
As shown in Equation 8, adopting a lower image amplification factor and higher temporal resolution can reduce the relative error. The image amplification factor is determined by the closest focusing distance of the camera’ s lens and the distance from the object plane to the lens. A shorter focusing distance and shorter shooting distance will decrease the image amplification factor. It should be particularly noted that a small Δ t (the time interval between two consecutive images) is better because large Δ t would make particles with high velocity more difficult to measure when the particle density in measured height area is also high.
Figure 3 shows two consecutive images of saltating particles with a time interval of Δ t=0.2× 10-3 s. As the photographs show, the particles have a low contrast with the background, especially near the surface. Figure 4 shows the results of particle recognition, i.e., the particles were clearly recognized when Equations 1 and 2 were applied.
 | Fig. 4 Results of the image analysis, showing the particles identified by the new particle tracking velocimetry method |
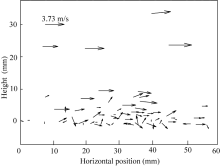
Particles can be recognized in each consecutive image. After the centroids of the particles have been located, an image of the particle centroids can be obtained. Based on the particle distribution shown in Figure 4, we divided the images into five height ranges above the surface (0-3, 3-5, 5-10, 10-20, and 20-40 mm), and separately processed the data for the particles in each height range. Figure 5 shows the resulting match efficiencies calculated using different dilation coefficients for each height range. We then used the optimal dilation coefficient determined from the data in Figure 5 and calculated a superposition image for the two consecutive particle centroid dilation images (Fig. 6). Using the optimal dilation factors for each height range, the particle centroids at heights of 0-3, 3-5, 5-10, 10-20, and 20-40 mm were enlarged to produce regular discs with characteristic particle diameters of 3, 2, 5, 5, and 7 pixels, respectively. Based on changes in the positions of the particle centroids in the overlapped image, Equation 5 can be used to calculate the instantaneous velocity for each particle, which can be graphed to show the instantaneous velocity field (Fig. 7).
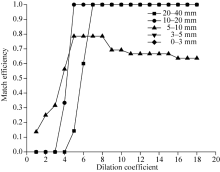 | Fig. 5 Match efficiency produced by different dilation coefficients for five height ranges above the surface |
 | Fig. 6 An example of the pairs of centroids produced by the overlapped dilation images. Horizontal lines represent the five height intervals shown in Figure 5. |
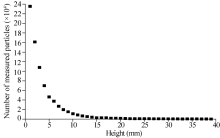
A blowing sand cloud is a special case of a two-phase gas-solid flow that consists of a large number of sand particles with different trajectories or at different stages in their trajectory (ascending or descending). Because these parameters vary with heights, the result is a map of horizontal and vertical velocities, i.e., a velocity field. Due to the short time interval (Δ t=0.0002 s) between the two image frames in Figure 7, that figure represents a nearly instantaneous velocity field. To determine the representative velocity distribution within a blowing sand cloud, we expanded the measurement time span. The particle density rapidly decreases with increasing height (Liu and Dong, 2004; Dong et al., 2006). This means that the number of particles measured at greater heights above the bed may be too few for analysis if the duration is too short. Unfortunately, the duration is limited by the available hard disk space. After many trial alculations, we found that 400 velocity records were sufficient to provide a stable probability distribution for particle velocities at a given height. Figure 8 shows the number of velocity records at different heights obtained from 20, 000 consecutive images (obtained within 4 s, for particles with d=0.1-0.2 mm, with U=6.5 m/s). Figure 8 shows that a total of nearly 800× 103 velocity records were measured using the new PTV algorithm, which provides a dramatic contrast with the maximum sample size of 21 in a previous study (Zou et al., 2001).
Figure 9 shows the ratio of the number of measured particles to the number of recognized particles as a function of height. The number of particles recognized at a given height is equivalent to the number of particle centroids at that height. Figure 9 shows that 72% to 99% of the identified saltating particles can be measured using the new PTV method. Thus, this method can provide a good representation of the characteristics of a cloud of saltating sand.
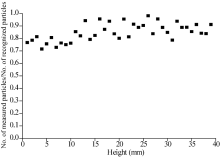 | Fig. 9 Ratio of the number of measured particles to the number of recognized particles as a function of height (d=0.1-0.2 mm, U=6.5 m/s) |
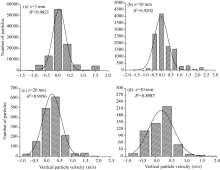
Rich information on the probability distribution of particle velocities can be obtained from the PTV measurement dataset. We have provided representative examples of the velocity distributions at four different heights. Figure 10 shows the horizontal velocity distribution and Figure 11 the vertical velocity distribution. These distributions are similar to those reported in previous studies (Greeley et al., 1983; White, 1985; Zou et al., 2001; Dong et al., 2004; Yang et al., 2007), but with many more particle samples used to calculate the distribution. The horizontal and vertical particle velocity distributions both fit the Gaussian or logistic distribution functions well (i.e., R2> 0.79, P< 0.05).
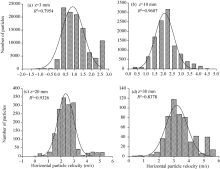 | Fig. 10 Typical probability distributions for horizontal particle velocity at four representative heights (z) with d=0.1-0.2 mm and U=6.5 m/s |
Variation of the mean velocity of a blowing sand as a function of height is an important factor in estimating the variations in its energy, momentum, sand transport rate, and erosivity (Zou et al., 2001). The mean velocity of a blowing sand cloud is calculated by:
$\overline{u}=\sum^{N-1}_{i=0}\frac{1}{N}u_{i}$; (8)
where N is the number of velocity samples, and ui is the velocity of sample i (m/s).
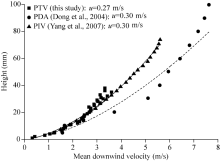
The horizontal velocity of saltating sand grains is mainly affected by the acceleration of the air flow, which is theoretically proportional to (uw-up)2, where uw is the horizontal wind velocity (m/s) and up is the horizontal particle velocity (m/s). Several techniques have been employed to measure the velocity of the blowing sand particles. The most commonly used methods include photoelectric cells, high-speed photography, PDA, and PIV. Several authors (Greeley et al., 1983; Zou et al., 2001; Dong et al., 2004; Yang et al., 2007) came to the same conclusion that the mean downwind velocity increases with increasing height following a power function and decreases with increasing grain size, but the predicted results differ widely. This is because each technique is based on certain unique principles, which have advantages and disadvantages that are reflected in the accuracy of the results.
Least-squares regression indicates that the changes in the mean horizontal downwind velocity of a saltation cloud as a function of height can be expressed using a power function:
$u=\alpha{Z^b}$, (9)
where u is the mean downwind velocity (m/s); Z is the height (mm) above the surface; and a and b are regression coefficients.
Figure 12 compares PDA results (Dong et al., 2004) and PIV results (Yang et al., 2007) with the present results obtained by high-speed photography under similar conditions. PDA results were very different from PIV results, even though both experiments were performed for particles with the same range of sizes and a similar wind velocity in the same wind tunnel. The curves initially follow similar paths, but at greater heights, the magnitudes of the predicted values differ greatly. The main difference between the two experiments was that natural quartz sand was used in the PDA experiment, whereas artificial quartz sand was used in the PIV experiment. This difference is probably not enough to explain the different magnitudes of the mean particle velocity. The primary cause of the differences is therefore likely to be the measurement methods. PIV is an optical method that captures the whole velocity field in part of the flow within a fraction of a millisecond, whereas PDA is a point-based measurement technique. Although the PDA system was precise and fast, its results for different parts of the flow field were not strictly simultaneous. In contrast, PIV results were close to the present results, especially at heights less than 20 mm above the surface. Both previous PIV and the improved new PTV methods are based on high-speed photography and can simultaneously measure the velocity of many particles at a range of heights. PIV produced less scattering than PTV in the results, probably because it produces an averaged velocity at a representative point in the interrogation window, whereas the new PTV technique allowed us to distinguish ascending particles from descending particles and to calculate their respective mean velocity fields.
The mean vertical velocity is, in most cases, much less than (< 10%) the mean horizontal downwind velocity (Fig. 13), being in agreement with wind tunnel results measured by PDA (Dong et al., 2004) and also with wind tunnel results measured by PIV (Yang et al., 2007). Because the mean vertical velocity is the average of the absolute values of both descending and ascending particles, the variation of the velocity in the vertical direction is much more complex than that in the downwind (horizontal) direction. In addition, factors such as rebounding from the bed and inter-particle collisions in air (Rice et al., 1995, 1996), combined with the lift force resulting from air turbulence, the Magnus effect, and other potentially unknown factors, further increase the complexity. Despite this complexity, the distribution of the mean vertical velocity as a function of height had a similar shape for the different size groups, though with different means and standard deviations (Fig. 11). At low (< 5 mm) heights, the net movement in the vertical direction tends to be upward, as indicated by the negative values of the mean vertical velocity (Fig. 13). At greater heights (> 5 mm), the net movement of particles in the vertical direction tends to be downward, as indicated by the positive values of the mean vertical velocity.
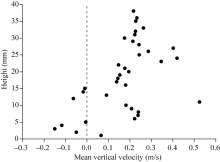 | Fig. 13 Variation in the mean vertical velocity of particles in a blowing sand cloud as a function of height |
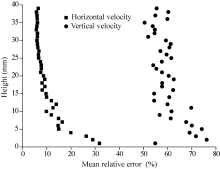
The precision of the estimated mean velocity at a certain height can be evaluated by the mean relative error of all measurements at that height. It should be noted that the mean relative errors are produced from the relative error distribution at a given height. The relative error of a particle’ s velocity can be estimated using Equation 6 (in this experiment, with Δ t=0.2× 10-3 s, σ =74.66× 10-6m/pixel). Figure 14 shows the results of mean relative errors of horizontal and vertical velocities. The mean relative error of horizontal velocity remains less than 35% at all heights, and decreases rapidly with increasing height. At heights above 3 mm, the error value remains less than 20%. As we know that obtaining the true mean velocity of an aeolian saltation cloud is impossible with current technology. For example, the mean velocity estimated by PDA (Dong et al. 2002b) was more than twice of that estimated by high-speed photography (Zou et al., 2001). Consequently, the low error range of the new PTV technique is acceptable. The mean relative errors of vertical velocity ranged from 50% to 80% and had no significant change with height. Although the mean vertical velocities obtained by the new PTV method have relative large errors, the new approach nonetheless permits a rough estimation of their values.
Particle turbulence (a dimensionless parameter) is defined as the fluctuation in velocity of wind-blown sand particles in a blowing sand cloud as it passes a fixed point. Turbulence is calculated as follows:
${{T}_{U}}=\frac{1}{{{U}_{p}}}\sqrt{\frac{\sum\limits_{i=1}^{N}{{{({{U}_{i}}-U)}^{2}}}}{N}}; \text{ }{{T}_{V}}=\frac{1}{{{V}_{p}}}\sqrt{\frac{\sum\limits_{i=1}^{N}{{{({{V}_{i}}-V)}^{2}}}}{N}}, $ (10)
where TU is the particle turbulence in the downwind direction; TV is the particle turbulence in the vertical direction; Up is the mean downwind particle velocity (m/s); Vp is the mean vertical particle velocity (m/s); Ui is the downwind velocity of particle i (m/s); Vi is the vertical velocity of particle i (m/s); and N is the number of velocity records.
Particle turbulence mainly results from the turbulence of the wind, impacts with the bed, and inter-particle collisions in air (Dong et al., 2004). Using the instantaneous horizontal and vertical velocities of each measured particle, the variation of particle turbulence can be calculated in both the downwind (horizontal) and vertical directions (Fig. 15).
Particle turbulence in the downwind direction (TU) generally decreases with increasing height at all free-stream wind velocities and for all size groups, suggesting that the wind’ s turbulence is the primary factor responsible for particle turbulence in the downwind direction. There was a sharp decrease in TU between the surface and a height of 3 mm (Fig. 15a). Figure 15b shows that the variation of particle turbulence in the vertical direction was about 10 times that in the downwind direction. The variation of its maximum value was nearly 10, 000%. As was the case for the variation in the vertical velocity of particles in a blowing sand cloud with height, the change of particle turbulence in the vertical direction (TV) as a function of height was complex. This suggests that impacts with the bed and inter-particle collisions in air may be the primary factors responsible for particle turbulence in the vertical direction.
In this study, we developed a new two-frame particle-tracking algorithm based on PTV for measuring the velocities of saltating particles. Using this method, it was possible to simultaneously extract the velocity of a large number of saltating particles at different heights (accounting for 72% to 99% of the total number of particles) from high-speed photographs. Rich information on the probability distribution of particle velocities was obtained from the PTV measurement dataset. Based on the velocity distribution in the horizontal and vertical directions, we produced a profile of the mean velocity. We evaluated the precision of the mean velocity estimates using the mean relative error. Above 3 mm in height, the mean relative errors for the horizontal velocity were less than 20%; above this height, the mean relative error ranged from 25% to 33%. Although the mean relative errors of the vertical velocity were much higher (ranging from 50% to 80%), the new technique nonetheless provided a rough estimate of the distribution of these values. In addition, it was possible to calculate the horizontal and vertical particle turbulence as a function of height based on a large number of individual particle velocities.
Although our results suggest that the improved new PTV technique is a generally reliable and useful method for calculating the velocity of saltating particles from high-speed photographs, some improvements are necessary. First, the method must be tested using saltation clouds with a much higher particle density produced by stronger winds. Second, we must look for ways to decrease the relative error in the vertical velocity measurements.
This work was funded by the Young Talent Fund of University Association for Science and Technology in Shaanxi, China (20170303), the National Science Basic Research Plan in Shaanxi Province of China (2017JQ6080), and the Talent Development Project of Weinan Normal University, China (16ZRRC02).
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|